
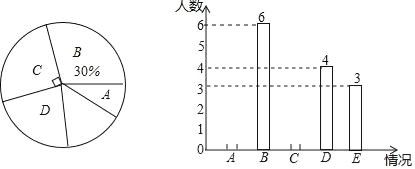
����Ŀ�����ų����ĵ�����ͬѧ�Ƕ�������ŵij�����̽Σ�Ϊ���˽��꼶ͬѧ��ÿ����ҵ���ʱ��������ֶ��꼶����ͬѧ���е���ͳ�ƣ����Ƴ�����������������ͳ��ͼ��������A���������ҵʱ��2Сʱ��B���������ҵʱ��2.5Сʱ��C���������ҵʱ��3Сʱ��D����˯��ʱ��3.5Сʱ��E����˯��ʱ��4Сʱ������������ͳ��ͼ����C����Բ�Ľ�Ϊ90����������ͳ��ͼ������Ϣ����������⣺
(1)����ȡ���� ����ͬѧ���е��飬ͬѧ�ǵ������ҵʱ�����λ������ ��Сʱ����������ͳ��ͼ����������
(2)��ȡ�����ͬѧ�У�D��ѧ����������Ů��E��ѧ��������һŮ����Ҫ��D��E����ѧ���и���ȡһ��ͬѧ���˽���ÿ��������ҵʱ�䰲�ŵľ�����������ȡ��������ѧ���պ���һ��һŮ�ĸ����Ƕ��٣�
���𰸡�(1)20��3����ͼ��������(2)![]() .
.
��������
��1����B���������������ռ�����ɵ����������ٷֱ����C��A��������������������λ���Ķ������ɵã�
��2���б��ó����п��ܵ�����������ҳ�һ��һŮ���������Ȼ����ݸ��ʹ�ʽ���ɵó��𰸣�
(1)����ȡ��ͬѧ����=6��30%=20���ˣ���
˯��ʱ��3Сʱ���ҵ�����![]() ���ˣ���˯��ʱ��2Сʱ����=20��6��5��4��3=2���ˣ���
���ˣ���˯��ʱ��2Сʱ����=20��6��5��4��3=2���ˣ���
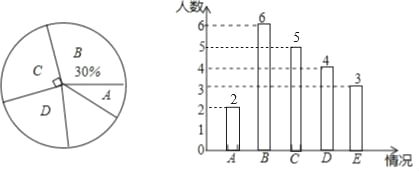
����˯��ʱ���С�������У����������ֱ�Ϊ2��6��5��4��3������20�����ݣ�
��10���͵�11�����ݶ���3Сʱ�����ǵ�ƽ����Ҳ��3Сʱ��
��ͬѧ�ǵ�˯��ʱ�����λ����3Сʱ���ң�
������ͳ��ͼ����������ͼ��ʾ��
(2)�б��ã�
�� | �� | ٠| |
�� | ���У��У� | ���У��У� | ���У�Ů�� |
�� | ���У��У� | ���У��У� | ���У�Ů�� |
Ů | ��Ů���У� | ���У�Ů�� | ��Ů��Ů�� |
Ů | ��Ů���У� | ���У�Ů�� | ��Ů��Ů�� |
���еȿ��ܵ������12�֣��պ���һ��һŮ��6�֣�
��ȡ��������ѧ���պ���һ��һŮ�ĸ�����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������һ���µĽ��ܲ�Ʒ���ò�Ʒ�ijɱ���Ϊ6Ԫ/�����ò�Ʒ����ʽͶ���г�ǰͨ�������������Ϊ��һ����(30��)�������ۣ��ۼ�Ϊ10Ԫ/����������Ա��������������˸��ټ�¼��������¼������Ƴ�ͼ��ͼ�е�����ABC��ʾ��������y(��)������ʱ��x(��)֮��ĺ�����ϵ��

(1)��y��x֮��ĺ�������ʽ����д��x��ȡֵ��Χ��
(2)���ý��ܲ�Ʒ������������ΪW(Ԫ)����W��x֮��ĺ�������ʽ�������������������1040Ԫ���������ж����죿
(3)��5��x��17��ֱ��д���ڼ�������������������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
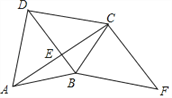
����Ŀ����ͼ���ı���ABCD�ĶԽ���AC��BD�ڵ�E��AB=BC��FΪ�ı���ABCD��һ�㣬�ҡ�FCA=90������CBF=��DCB��
��1����֤���ı���DBFC��ƽ���ı��Σ�
��2�����BCƽ�֡�DBF����CDB=45����BD=2����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽���� ��ͼ��ֱ��![]() �ı���ʽΪ
�ı���ʽΪ![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��
��1�����![]() �����ꣻ
�����ꣻ
��2����ֱ��![]() �ı���ʽ��
�ı���ʽ��
��3����![]() ��ֵ��
��ֵ��
��4����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ���ֱ��д����
�������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ѧ�е���������ϣ�Ҳ����������о�����������һ�������¿��Ի���ת��.���ν�Ͼ��ǰѳ������ѧ���ԡ�������ϵ��ֱ�۵ļ���ͼ�Ρ�λ�ù�ϵ���������ͨ������������������������������ͨ������˼ά������˼ά�Ľ�ϣ�����ʹ���������������������廯���Ӷ����Ż�����;����Ŀ��.
(1) ��˼��Ӧ�ã���֪m�� n��Ϊ��ʵ������m+n=2��![]() ����Сֵͨ����������˼����С���뵽����������Ĺ�����������:��ͼ�� AB=2��AC=1��BD=2��AC��AB��BD��AB����E���߶�AB�ϵĶ��㣬�Ҳ���˵��غϣ�����CE��DE����AE=m�� BE=n.
����Сֵͨ����������˼����С���뵽����������Ĺ�����������:��ͼ�� AB=2��AC=1��BD=2��AC��AB��BD��AB����E���߶�AB�ϵĶ��㣬�Ҳ���˵��غϣ�����CE��DE����AE=m�� BE=n.
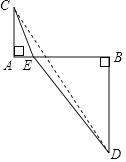
���ú�m�Ĵ���ʽ��ʾCE=_______�� �ú�n�Ĵ���ʽ��ʾDE= ;
�ھݴ���![]() ����Сֵ;
����Сֵ;
(2)�����Ӧ�ã����������ķ����������ʽ![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
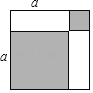
����Ŀ����1����ϸ�۲���ͼͼ�Σ����������ϵд��һ����ʽ��a2+b2���� ����
��2�����ݣ�1���еĵ�ʽ��ϵ������⣺��֪m+n��4��mn����2����m2+n2��ֵ��
��3��С�����ݣ�1���еĹ�ϵʽ��������������⣺
����֪m+![]() ��3����m2+
��3����m2+![]() ��m3+
��m3+![]() ��ֵ��
��ֵ��
С���ⷨ��
![]()
![]()
![]()
������ϸ����С���Ľⷨ��������ɣ���m5+m��5��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺��y��z��2+��x��y��2+��z��x��2=��y+z��2x��2+��z+x��2y��2+��x+y��2z��2��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ8���ı���ABEG��GEFH��HFCD���DZ߳�Ϊ1��������.
��1����֤����AEF�ס�CEA��
��2����֤����AFB+��ACB=45��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(10��) ��ͼ��С����һ�ű߳�Ϊ![]() ����������Ӳֽ������ܸ���ȥһ��ͬ����С�������Σ����ۺϳ�һ���ǵij�������ӣ�
����������Ӳֽ������ܸ���ȥһ��ͬ����С�������Σ����ۺϳ�һ���ǵij�������ӣ�

��1�����Ҫ������ӵĵ������Ϊ![]() �����ȥ��С�����α߳�Ϊ���٣�
�����ȥ��С�����α߳�Ϊ���٣�
��2����������ӵIJ�����Ƿ����Ϊ![]() ��Ϊʲô��
��Ϊʲô��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com