
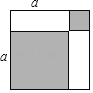
【题目】(1)仔细观察如图图形,利用面积关系写出一个等式:a2+b2= .
(2)根据(1)中的等式关系解决问题:已知m+n=4,mn=﹣2,求m2+n2的值.
(3)小明根据(1)中的关系式还解决了以下问题:
“已知m+![]() =3,求m2+
=3,求m2+![]() 和m3+
和m3+![]() 的值”
的值”
小明解法:
![]()
![]()
![]()
请你仔细理解小明的解法,继续完成:求m5+m﹣5的值
【答案】(1)(a+b)2﹣2ab;(2)20;(3)123
【解析】
(1)观察原式为阴影部分的面积,再用大矩形的面积减去两个空白矩形的面积也可表示阴影部分面积,进而得出答案;
(2)运用(1)中的结论进行计算便可把原式转化为(m+n)2﹣2mn进行计算;
(3)把原式转化为(m2+m﹣2)(m3+m﹣3)﹣(m+m﹣1)进行计算.
解:(1)根据图形可知,阴影部分面积为a2+b2,
阴影部分面积可能表示为(a+b)2﹣2ab,
∴a2+b2=(a+b)2﹣2ab,
故答案为:(a+b)2﹣2ab;
(2)m2+n2=(m+n)2﹣2mn=42﹣2×(﹣2)=20;
(3)m5+m﹣5=(m2+m﹣2)(m3+m﹣3)﹣(m+m﹣1)=7×18﹣3=123.


科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,鼓楼区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中某些家庭一年的月平均用水量(单位:吨),调查中发现,每户用水量每月均在10﹣14吨范围,并将调查结果制成了如图所示的条形统计图(不完整)和扇形统计图.

(1)请将条形统计图补充完整;
(2)这些家庭月用水量数据的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计鼓楼区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA=2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=8,BC=12,点E是边BC上一点,BE=5,点F是射线BA上一动点,连接EF,将△BEF沿着EF折叠,使B点的对应点P落在长方形一边的垂直平分线上,连接BP,则BP的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
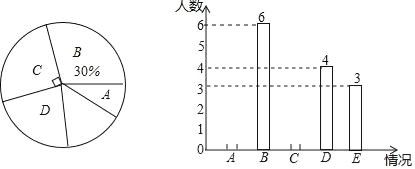
【题目】随着初三的到来,同学们都进入紧张的初三冲刺阶段,为了了解年级同学们每天作业完成时间情况,现对年级部分同学进行调查统计,并制成如下两幅不完整的统计图:(其中A代表完成作业时间2小时,B代表完成作业时间2.5小时,C代表完成作业时间3小时,D代表睡眠时间3.5小时,E代表睡眠时间4小时),其中扇形统计图中“C”的圆心角为90°,请你结合统计图所给信息解答下列问题:
(1)共抽取了 名同学进行调查,同学们的完成作业时间的中位数是 小时,并将条形统计图补充完整;
(2)抽取调查的同学中,D类学生有两男两女,E类学生有两男一女,现要从D、E两类学生中各抽取一名同学,了解其每天晚上作业时间安排的具体情况,则抽取到的两名学生刚好是一男一女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式;
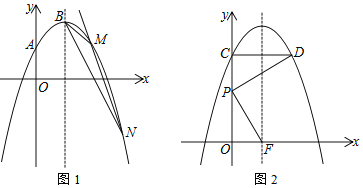
(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投入研发费用80万元![]() 万元只计入第一年成本
万元只计入第一年成本![]() ,成功研发出一种产品
,成功研发出一种产品![]() 公司按订单生产
公司按订单生产![]() 产量
产量![]() 销售量
销售量![]() ,第一年该产品正式投产后,生产成本为6元
,第一年该产品正式投产后,生产成本为6元![]() 件
件![]() 此产品年销售量
此产品年销售量![]() 万件
万件![]() 与售价
与售价![]() 元
元![]() 件
件![]() 之间满足函数关系式
之间满足函数关系式![]() .
.
![]() 求这种产品第一年的利润
求这种产品第一年的利润![]() 万元
万元![]() 与售价
与售价![]() 元
元![]() 件
件![]() 满足的函数关系式;
满足的函数关系式;
![]() 该产品第一年的利润为20万元,那么该产品第一年的售价是多少?
该产品第一年的利润为20万元,那么该产品第一年的售价是多少?
![]() 第二年,该公司将第一年的利润20万元
第二年,该公司将第一年的利润20万元![]() 万元只计入第二年成本
万元只计入第二年成本![]() 再次投入研发,使产品的生产成本降为5元
再次投入研发,使产品的生产成本降为5元![]() 件
件![]() 为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件
为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件![]() 请计算该公司第二年的利润
请计算该公司第二年的利润![]() 至少为多少万元.
至少为多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
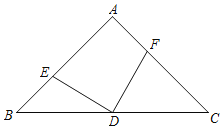
【题目】如图,在等腰直角△ABC中,∠A=90°,AB=AC,D为边BC中点,DE⊥DF,若四边形AEDF的面积是4,则等腰直角△ABC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△FGH中,D、E两点分别在AB、AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为何?( )

A. 2:1 B. 3:2 C. 5:2 D. 9:4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com