
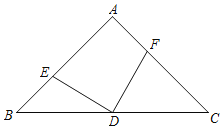
【题目】如图,在等腰直角△ABC中,∠A=90°,AB=AC,D为边BC中点,DE⊥DF,若四边形AEDF的面积是4,则等腰直角△ABC的面积为_____.
科目:初中数学 来源: 题型:
【题目】亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部![]() , 颖颖的头顶
, 颖颖的头顶![]() 及亮亮的眼睛
及亮亮的眼睛![]() 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置![]() ,
, ![]() . 然后测出两人之间的距离
. 然后测出两人之间的距离![]() , 颖颖与楼之间的距离
, 颖颖与楼之间的距离![]() (
(![]() ,
, ![]() ,
, ![]() 在一条直线上),颖颖的身高
在一条直线上),颖颖的身高![]() , 亮亮蹲地观测时眼睛到地面的距离
, 亮亮蹲地观测时眼睛到地面的距离![]() . 你能根据以上测量数据帮助他们求出住宅楼的高度吗?
. 你能根据以上测量数据帮助他们求出住宅楼的高度吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
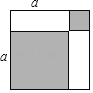
【题目】(1)仔细观察如图图形,利用面积关系写出一个等式:a2+b2= .
(2)根据(1)中的等式关系解决问题:已知m+n=4,mn=﹣2,求m2+n2的值.
(3)小明根据(1)中的关系式还解决了以下问题:
“已知m+![]() =3,求m2+
=3,求m2+![]() 和m3+
和m3+![]() 的值”
的值”
小明解法:
![]()
![]()
![]()
请你仔细理解小明的解法,继续完成:求m5+m﹣5的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出命题“等腰三角形底边上的角平分线与中线互相重合”的逆命题,并用推理的方法证明你所写的这个逆命题是真命题.
逆命题:___________________;
已知:____________________;
求证:___________________.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,四边形ABEG、GEFH、HFCD都是边长为1的正方形.
(1)求证:△AEF∽△CEA;
(2)求证:∠AFB+∠ACB=45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 为
为![]() 上的两个定点,
上的两个定点,![]() 是
是![]() 上的动点(
上的动点(![]() 不与
不与![]() 、
、![]() 重合),我们称
重合),我们称![]() 为
为![]() 上关于点
上关于点![]() 、
、![]() 的滑动角.已知
的滑动角.已知![]() 是
是![]() 上关于点
上关于点![]() 、
、![]() 的滑动角,
的滑动角,
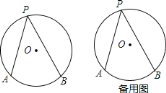
(1)若![]() 为
为![]() 的直径,则
的直径,则![]() ________;
________;
(2)若![]() 半径为
半径为![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() 半径为
半径为![]() ,
,![]() ,
,![]() ,求
,求
查看答案和解析>>
科目:初中数学 来源: 题型:
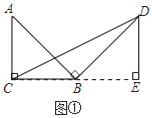
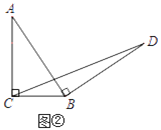
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
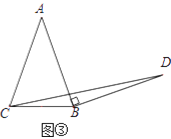
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
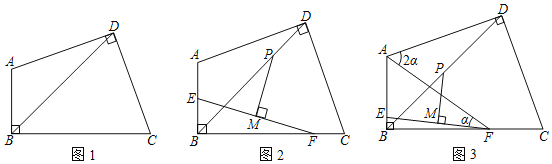
【题目】如图1,四边形ABCD中,∠ABC=∠ADC=90°,AD=CD.
(1)求证:BD平分∠ABC;
(2)如图2,点E、F分别在AB、BC上,连接EF,M是EF的中点,过M作EF的垂线交BD于P.求证:AE+CF=![]() PD;
PD;
(3)如图3,在(2)条件下,连AF,若AE=CF,∠DAF=2∠AFE=2α,AF=13,BC=12![]() ,(BC>AB).求BD的长.
,(BC>AB).求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com