
【题目】抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式;
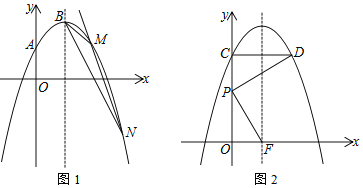
(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
【答案】(1)y=﹣x2+2x+1;(2)-3;(3)当m=2![]() ﹣1时,点P的坐标为(0,
﹣1时,点P的坐标为(0,![]() )和(0,
)和(0,![]() );当m=2时,点P的坐标为(0,1)和(0,2).
);当m=2时,点P的坐标为(0,1)和(0,2).
【解析】
(1)根据对称轴为直线x=1且抛物线过点A(0,1)利用待定系数法进行求解可即得;
(2)根据直线y=kx﹣k+4=k(x﹣1)+4知直线所过定点G坐标为(1,4),从而得出BG=2,由S△BMN=S△BNG﹣S△BMG=![]() BGxN﹣
BGxN﹣![]() BGxM=1得出xN﹣xM=1,联立直线和抛物线解析式求得x=
BGxM=1得出xN﹣xM=1,联立直线和抛物线解析式求得x=![]() ,根据xN﹣xM=1列出关于k的方程,解之可得;
,根据xN﹣xM=1列出关于k的方程,解之可得;
(3)设抛物线L1的解析式为y=﹣x2+2x+1+m,知C(0,1+m)、D(2,1+m)、F(1,0),再设P(0,t),分△PCD∽△POF和△PCD∽△POF两种情况,由对应边成比例得出关于t与m的方程,利用符合条件的点P恰有2个,结合方程的解的情况求解可得.
(1)由题意知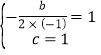 ,解得:
,解得:![]() ,
,
∴抛物线L的解析式为y=﹣x2+2x+1;
(2)如图1,设M点的横坐标为xM,N点的横坐标为xN,
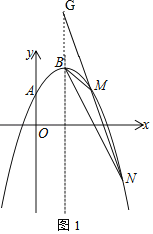
∵y=kx﹣k+4=k(x﹣1)+4,
∴当x=1时,y=4,即该直线所过定点G坐标为(1,4),
∵y=﹣x2+2x+1=﹣(x﹣1)2+2,
∴点B(1,2),
则BG=2,
∵S△BMN=1,即S△BNG﹣S△BMG=![]() BG(xN﹣1)-
BG(xN﹣1)-![]() BG(xM-1)=1,
BG(xM-1)=1,
∴xN﹣xM=1,
由![]() 得:x2+(k﹣2)x﹣k+3=0,
得:x2+(k﹣2)x﹣k+3=0,
解得:x=![]() =
=![]() ,
,
则xN=![]() 、xM=
、xM=![]() ,
,
由xN﹣xM=1得![]() =1,
=1,
∴k=±3,
∵k<0,
∴k=﹣3;
(3)如图2,

设抛物线L1的解析式为y=﹣x2+2x+1+m,
∴C(0,1+m)、D(2,1+m)、F(1,0),
设P(0,t),
(a)当△PCD∽△FOP时,![]() ,
,
∴![]() ,
,
∴t2﹣(1+m)t+2=0①;
(b)当△PCD∽△POF时,![]() ,
,
∴![]() ,
,
∴t=![]() (m+1)②;
(m+1)②;
(Ⅰ)当方程①有两个相等实数根时,
△=(1+m)2﹣8=0,
解得:m=2![]() ﹣1(负值舍去),
﹣1(负值舍去),
此时方程①有两个相等实数根t1=t2=![]() ,
,
方程②有一个实数根t=![]() ,
,
∴m=2![]() ﹣1,
﹣1,
此时点P的坐标为(0,![]() )和(0,
)和(0,![]() );
);
(Ⅱ)当方程①有两个不相等的实数根时,
把②代入①,得:![]() (m+1)2﹣
(m+1)2﹣![]() (m+1)+2=0,
(m+1)+2=0,
解得:m=2(负值舍去),
此时,方程①有两个不相等的实数根t1=1、t2=2,
方程②有一个实数根t=1,
∴m=2,此时点P的坐标为(0,1)和(0,2);
综上,当m=2![]() ﹣1时,点P的坐标为(0,
﹣1时,点P的坐标为(0,![]() )和(0,
)和(0,![]() );
);
当m=2时,点P的坐标为(0,1)和(0,2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
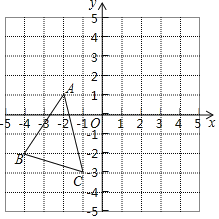
【题目】如图,△ABC中,A(-2,1),B(-4,-2),C(-1,-3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′______,B′______;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相同,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各种多少两?设黄金重![]() 两,每枚白银重
两,每枚白银重![]() 两,根据题意可列方程组为____.
两,根据题意可列方程组为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).
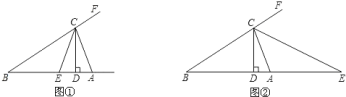
(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数(直接写出结果);
(3)如图②,若CE是△ABC外角∠ACF的平分线,交BA延长线于点E,且α﹣β=30°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“8字”的性质及应用:
(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
(2)图②中共有多少个“8字”?
(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=![]() (∠A+∠C).
(∠A+∠C).

查看答案和解析>>
科目:初中数学 来源: 题型:
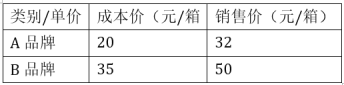
【题目】列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
(1)该大型超市购进A、B品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )

A. ①③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有一长条型链子,其外形由边长为![]() 的正六边形排列而成.其中每个黑色六边形与6个白色六边形相邻,若链子上有35个黑色六边形,则此链子有( )个白色六边形.
的正六边形排列而成.其中每个黑色六边形与6个白色六边形相邻,若链子上有35个黑色六边形,则此链子有( )个白色六边形.

A.140B.142C.208D.210
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com