
【题目】如图①,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).
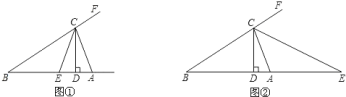
(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数(直接写出结果);
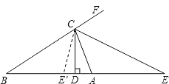
(3)如图②,若CE是△ABC外角∠ACF的平分线,交BA延长线于点E,且α﹣β=30°,求∠DCE的度数.
【答案】(1)15°;(2)![]() ;(3)75°.
;(3)75°.
【解析】
(1)三角形的内角和是180°,已知∠BAC与∠ABC的度数,则可求出∠BAC的度数,然后根据角平分线的性质求出∠BCE,再利用三角形的一个外角等于和它不相邻的两个内角的和求出∠DEC的度数,进而求出∠DCE的度数;
(2)∠DCE=![]() .
.
(3)作∠ACB的内角平分线CE′,根据角平分线的性质求出∠ECE′=∠ACE+∠ACE′=![]() ∠ACB+
∠ACB+![]() ∠ACF=90°,进而求出∠DCE的度数.
∠ACF=90°,进而求出∠DCE的度数.
解:(1)因为∠ACB=180°﹣(∠BAC+∠B)=180°﹣(70°+40°)=70°,
又因为CE是∠ACB的平分线,
所以![]() .
.
因为CD是高线,
所以∠ADC=90°,
所以∠ACD=90°﹣∠BAC=20°,
所以∠DCE=∠ACE﹣∠ACD=35°﹣20°=15°.
(2)![]() .
.
(3)如图,作∠ACB的内角平分线CE′,
则![]() .
.
因为CE是∠ACB的外角平分线,
所以∠ECE′=∠ACE+∠ACE′=![]() =
=![]() =90°,
=90°,
所以∠DCE=90°﹣∠DCE′=90°﹣15°=75°.
即∠DCE的度数为75°.


科目:初中数学 来源: 题型:
【题目】某服装销售店到生产厂家选购A,B两种品牌的服装,若购进A品牌服装1套,B品牌服装1套,共需205元;若购进A品牌服装2套,B品牌服装3套,共需495元.
(1)求A,B两种品牌的服装每套进价分别为多少元?
(2)若A品牌服装每套售价为150元,B品牌服装每套售价为100元,根据市场的需求,现决定购进B品牌服装数量比A品牌服装数量的2倍还多3套.如果购进B品牌服装不多于47套,且服装全部售出后,获利总额不少于1245元,问共有哪几种进货方案?哪种进货方案获利最多?最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,过顶点A的直线DE∥BC,∠ABC、∠ACB的平分线分别交DE于点E、D,若AC=3,AB=4,则DE的长为( )

A. 6B. 7C. 8D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五一期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:

(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
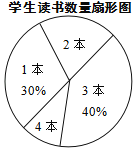
【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为1的正方形纸片分割成7个部分,第①部分是边长不1的正方形纸片面积的一半,第②部分是第①部分面积的半,第③部分是第③部分面积的一半,…,依次类推.
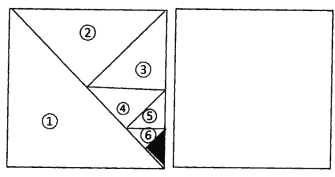
(1)阴影部分的面积是多少?
(2)受此启发,你能求出![]() 的值吗?
的值吗?
(3)请你利用图中右侧的正方形,再设计能求![]() 的值的几何图形.(只画出图形即可)
的值的几何图形.(只画出图形即可)
(4)根据以上规律,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
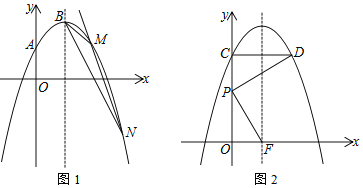
【题目】抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式;
(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
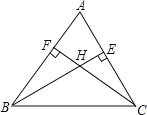
【题目】在△ABC中,已知∠ABC=60°,∠ACB=50°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点.求∠ABE、∠ACF和∠BHC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com