
����Ŀ��ij��װ���۵굽��������ѡ��A��B����Ʒ�Ƶķ�װ��������AƷ�Ʒ�װ1�ף�BƷ�Ʒ�װ1�ף�����205Ԫ��������AƷ�Ʒ�װ2�ף�BƷ�Ʒ�װ3�ף�����495Ԫ��
��1����A��B����Ʒ�Ƶķ�װÿ���۷ֱ�Ϊ����Ԫ��
��2����AƷ�Ʒ�װÿ���ۼ�Ϊ150Ԫ��BƷ�Ʒ�װÿ���ۼ�Ϊ100Ԫ�������г��������־�������BƷ�Ʒ�װ������AƷ�Ʒ�װ������2������3�ף��������BƷ�Ʒ�װ������47�ף��ҷ�װȫ���۳������ܶ����1245Ԫ���ʹ����ļ��ֽ������������ֽ�������������ࣿ����Ƕ��٣�
���𰸡���1��A��Ʒ�Ƶķ�װÿ����Ϊ120Ԫ��B��Ʒ�Ƶķ�װÿ����Ϊ85Ԫ����2�������ַ���������һ������A��Ʒ�Ʒ�װ20�ף�B��Ʒ�Ʒ�װ43�ף�������������A��Ʒ�Ʒ�װ21�ף�B��Ʒ�Ʒ�װ45�ף�������������A��Ʒ�Ʒ�װ22�ף�B��Ʒ�Ʒ�װ47�ף�����A��Ʒ�Ʒ�װ22�ף�B��Ʒ�Ʒ�װ47��ʱ��������࣬�����1365Ԫ��
��������
��1����A��Ʒ�Ƶķ�װÿ����ΪxԪ��B��Ʒ�Ƶķ�װÿ����ΪyԪ��������������AƷ�Ʒ�װ1�ף�BƷ�Ʒ�װ1�ף�����205Ԫ��������AƷ�Ʒ�װ2�ף�BƷ�Ʒ�װ3�ף�����495Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2���蹺��A��Ʒ�Ʒ�װm�ף���B��Ʒ�Ʒ�װ![]() �ף����ݹ���BƷ�Ʒ�װ������47���ҷ�װȫ���۳�������ܶ����1245Ԫ�����ɵó�����m��һԪһ�β���ʽ�飬��֮���ɵó�m��ȡֵ��Χ�����mΪ�������ɵó�����������������������������������ȽϺɵó����ۣ�
�ף����ݹ���BƷ�Ʒ�װ������47���ҷ�װȫ���۳�������ܶ����1245Ԫ�����ɵó�����m��һԪһ�β���ʽ�飬��֮���ɵó�m��ȡֵ��Χ�����mΪ�������ɵó�����������������������������������ȽϺɵó����ۣ�
��1����A��Ʒ�Ƶķ�װÿ����ΪxԪ��B��Ʒ�Ƶķ�װÿ����ΪyԪ
������ã�![]()
��ã�![]()
��A��Ʒ�Ƶķ�װÿ����Ϊ120Ԫ��B��Ʒ�Ƶķ�װÿ����Ϊ85Ԫ��
��2���蹺��A��Ʒ�Ʒ�װm�ף���B��Ʒ�Ʒ�װ![]() ��
��
������ã�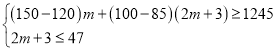
��ã�![]()
��m����
��![]()
��![]()
�������ַ���������һ������A��Ʒ�Ʒ�װ20�ף�B��Ʒ�Ʒ�װ43�ף�������������A��Ʒ�Ʒ�װ21�ף�B��Ʒ�Ʒ�װ45�ף�������������A��Ʒ�Ʒ�װ22�ף�B��Ʒ�Ʒ�װ47�ף����ַ���������ֱ����£�
![]() ��Ԫ��
��Ԫ��
![]() ��Ԫ��
��Ԫ��
![]() ��Ԫ��
��Ԫ��
��![]()
�ʹ���A��Ʒ�Ʒ�װ22�ף�B��Ʒ�Ʒ�װ47��ʱ��������࣬�����1365Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a�����ĸ�������b��c����![]() ����a��b��c�ֱ��ǵ�A��B��C�������϶�Ӧ������
����a��b��c�ֱ��ǵ�A��B��C�������϶�Ӧ������
(1)��a��b��c��ֵ�����������ϱ����A��B��C��
![]()
(2)������P��C�����������������˶�����P���ٶ���ÿ��2����λ���ȣ��˶������P����B��?
(3)����������һ��M��ʹ��M��A��B��C����ľ���֮�͵���13����ֱ��д�����е�M��Ӧ������(����˵������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����MΪֱ��AB��һ���㣬 ![]() ���ǵȱ������Σ�����BN
���ǵȱ������Σ�����BN
![]() ��֤��
��֤�� ![]() ��
��
![]() �ֱ�д����M����ͼ2��ͼ3��ʾλ��ʱ���߶�AB��BM��BN����֮���������ϵ
�ֱ�д����M����ͼ2��ͼ3��ʾλ��ʱ���߶�AB��BM��BN����֮���������ϵ![]() ����֤��
����֤��![]() ��
��
![]() ��ͼ4����
��ͼ4����![]() ʱ��֤����
ʱ��֤���� ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC������C=90������D��BC�ߵ��е���BD=2��tanB=![]() ��
��
��1����AD��AB�ij���
��2����sin��BAD��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
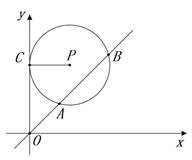
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���P��Բ���ǣ�2��a����a >0�����뾶��2����y�������ڵ�C��ֱ��y=x����P�صõ���AB�ij�Ϊ![]() ����a��ֵ�ǣ� ��
����a��ֵ�ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��l1�ĺ�����ϵʽΪy=2x+b��ֱ��l2��ԭ������ֱ��l1���ڵ�P��-1��-5����
��1�����ʣ�-1��-5�����Կ����������Ķ�Ԫһ�η�����Ľ⣿
��2����ֱ��l1��ֱ��y=x���ڵ�A�����APO�������
��3����x�����Ƿ���ڵ�Q��ʹ�á�AOQ�ǵ��������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
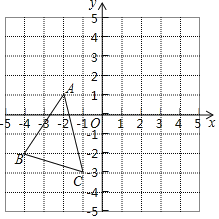
����Ŀ����ͼ����ABC�У�A(-2��1)��B(-4��-2)��C(-1��-3)����A��B��C���ǡ�ABCƽ��֮��õ���ͼ����C�Ķ�Ӧ��C��������Ϊ(4��1)
(1)A����B�����������ֱ�ΪA��______��B��______��
(2)������ABCƽ��֮���ͼ�Ρ�A��B��C����
(3)���ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ڡ�ABC�У�CD��CE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ���BAC��������B����������������
��1��������70�㣬����40�㣬���DCE�Ķ�����
��2�������������Ĵ���ʽ��ʾ��DCE�Ķ�����ֱ��д���������
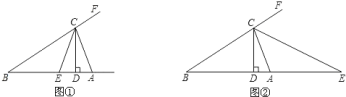
��3����ͼ������CE�ǡ�ABC��ǡ�ACF��ƽ���ߣ���BA�ӳ����ڵ�E������������30�㣬���DCE�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com