
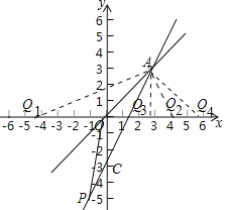
【题目】在平面直角坐标系中,直线l1的函数关系式为y=2x+b,直线l2过原点且与直线l1交于点P(-1,-5).
(1)试问(-1,-5)可以看作是怎样的二元一次方程组的解?
(2)设直线l1与直线y=x交于点A,求△APO的面积;
(3)在x轴上是否存在点Q,使得△AOQ是等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)(-1,-5)可以看成二元一次方程组![]() 的解;(2)S△AOP=6;(3)存在,点Q坐标为(-3
的解;(2)S△AOP=6;(3)存在,点Q坐标为(-3![]() ,0)或(3,0)或(3
,0)或(3,0)或(3![]() ,0)或(6,0).
,0)或(6,0).
【解析】
(1)求出直线![]() 与直线
与直线![]() 的解析式即可解决问题;
的解析式即可解决问题;
(2)利用方程组求出点A坐标,再求出直线![]() 与y轴的交点C的坐标,然后根据
与y轴的交点C的坐标,然后根据![]() 计算即可;
计算即可;
(3)根据等腰三角形的定义,分![]() 三种情形,然后利用两点之间的距离公式分别求解即可.
三种情形,然后利用两点之间的距离公式分别求解即可.
(1)∵点![]() 在直线
在直线![]() 上
上
![]() ,解得
,解得![]()
∴直线![]() 的解析式为
的解析式为![]()
设直线![]() 的解析式为
的解析式为![]()
则有![]() ,解得
,解得![]()
∴直线![]() 的解析式为
的解析式为![]()
故![]() 可以看成二元一次方程组
可以看成二元一次方程组![]() 的解;
的解;
(2)由![]() ,解得
,解得![]()
![]()
∵点![]() 在直线
在直线![]() 上,直线
上,直线![]() 交y轴于
交y轴于![]()
![]()
故![]() 的面积为6;
的面积为6;
(3)![]()
![]()
设点Q坐标为![]()
由等腰三角形的定义,分以下三种情况:
①当![]() 时,则
时,则![]() ,即
,即![]()
②当![]() 时,则
时,则![]()
解得![]() ,即
,即![]()
③当![]() 时,则
时,则![]()
解得![]() 或
或![]() (与点O重合,舍去),即
(与点O重合,舍去),即![]()
综上,满足条件的点Q坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
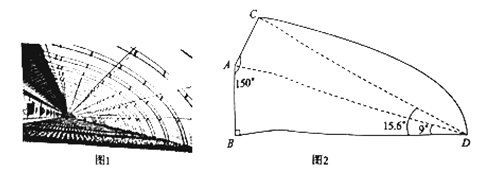
【题目】随着我市农产品整体品牌形象“聊·胜一筹!”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图1.线段![]() ,
,![]() 分别表示大棚的墙高和跨度,
分别表示大棚的墙高和跨度,![]() 表示保温板的长.已知墙高
表示保温板的长.已知墙高![]() 为2米,墙面与保温板所成的角
为2米,墙面与保温板所成的角![]() ,在点
,在点![]() 处测得
处测得![]() 点、
点、![]() 点的仰角分别为
点的仰角分别为![]() ,
,![]() ,如图2.求保温板
,如图2.求保温板![]() 的长是多少米?(精确到0.1米)
的长是多少米?(精确到0.1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装销售店到生产厂家选购A,B两种品牌的服装,若购进A品牌服装1套,B品牌服装1套,共需205元;若购进A品牌服装2套,B品牌服装3套,共需495元.
(1)求A,B两种品牌的服装每套进价分别为多少元?
(2)若A品牌服装每套售价为150元,B品牌服装每套售价为100元,根据市场的需求,现决定购进B品牌服装数量比A品牌服装数量的2倍还多3套.如果购进B品牌服装不多于47套,且服装全部售出后,获利总额不少于1245元,问共有哪几种进货方案?哪种进货方案获利最多?最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
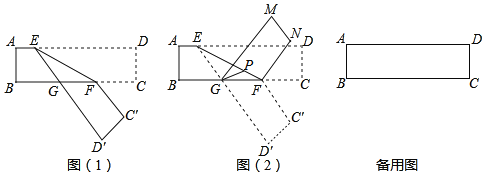
【题目】如图为长方形纸带,AD平行BC,E、F分别是边AD、BC上一点,∠DEF=α,α为锐角且α≠60°,将纸带沿EF折叠如图(1),再由GF折叠如图(2),若GP平分∠MGF交直线EF于点P,则∠GPE=_____(含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
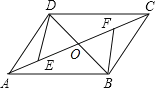
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为1的正方形纸片分割成7个部分,第①部分是边长不1的正方形纸片面积的一半,第②部分是第①部分面积的半,第③部分是第③部分面积的一半,…,依次类推.
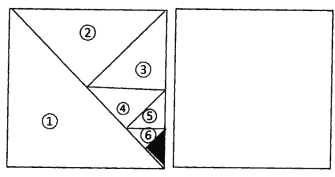
(1)阴影部分的面积是多少?
(2)受此启发,你能求出![]() 的值吗?
的值吗?
(3)请你利用图中右侧的正方形,再设计能求![]() 的值的几何图形.(只画出图形即可)
的值的几何图形.(只画出图形即可)
(4)根据以上规律,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com