
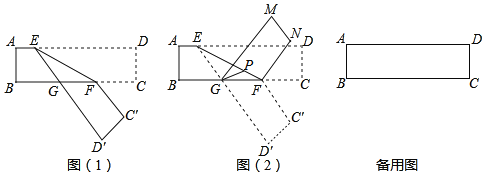
【题目】如图为长方形纸带,AD平行BC,E、F分别是边AD、BC上一点,∠DEF=α,α为锐角且α≠60°,将纸带沿EF折叠如图(1),再由GF折叠如图(2),若GP平分∠MGF交直线EF于点P,则∠GPE=_____(含α的式子表示)
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是

A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
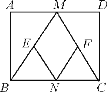
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB与AD满足什么条件时,四边形MENF是正方形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l1的函数关系式为y=2x+b,直线l2过原点且与直线l1交于点P(-1,-5).
(1)试问(-1,-5)可以看作是怎样的二元一次方程组的解?
(2)设直线l1与直线y=x交于点A,求△APO的面积;
(3)在x轴上是否存在点Q,使得△AOQ是等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且PE交边CD于点E.
(1)求证:PB=PE;
(2)过点E作EF⊥AC于点F,如图2.若正方形ABCD的边长为2,则在点P运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象交于点(2,1).
的图象与一次函数y=kx+m的图象交于点(2,1).
(1)分别求出这两个函数的解析式;
(2)判断P(﹣1,﹣5)是否在一次函数y=kx+m的图象上,并说明原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛,其预赛成绩如图:
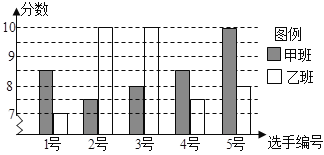
(1)根据上图求出下表中的a,b,c的值(单位:分);
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
(2)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛,求这5人预赛成绩的平均分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
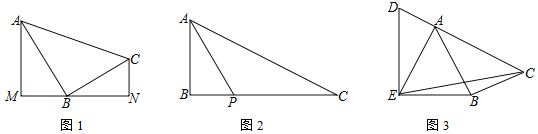
【题目】在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=![]() ,求tanC的值;
,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=![]() ,
,![]() ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com