【题目】已知反比例函数y=
的图象与一次函数y=kx+m的图象交于点（2，1）．
（1）分别求出这两个函数的解析式；
（2）判断P（﹣1，﹣5）是否在一次函数y=kx+m的图象上，并说明原因．
【答案】（1）y=
和y=2x﹣3．（2）点P在一次函数图象上.
【解析】（1）将点（2，1）代入y=
，求出k的值，再将k的值和点（2，1）代入解析式y=kx+m，即可求出m的值，从而得到两个函数的解析式；
（2）将x=-1代入（1）中所得解析式，若y=-5，则点P（-1，-5）在一次函数图象上，否则不在函数图象上．
（1）∵y=经过（2，1），
∴2=k．
∵y=kx+m经过（2，1），
∴1=2×2+m，
∴m=-3．
∴反比例函数和一次函数的解析式分别是：y=和y=2x-3．
（2）点P（-1，-5）在一次函数y=2x-3图象上．原因如下：
当x=-1时，y=2x-3=2×（-1）-3=-5．
∴点P（-1，-5）在一次函数图象上．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，O为坐标原点，△ABC 的顶点 A (-2,0),点 B，C分别在x轴和y轴的正半轴上,∠ACB=90°,∠BAC=60°
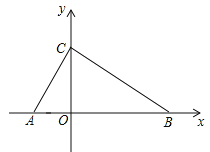
(1)求点 B 的坐标;
(2)点 P 为 AC延长线上一点，过 P 作PQ∥x轴交 BC 的延长线于点 Q ,若点 P 的横坐标为t，线段PQ的长为d，请用含t的式子表示d;
(3) 在（2）的条件下，当PA=
d时，E是线段CQ上一点，连接OE，BP，若OE=BP，求∠APB-∠OEB的度数．.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，定义：在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα=
=
，根据上述角的余切定义，解下列问题：
（1）如图1，若BC=3，AB=5，则ctanB= ；
（2）ctan60°= ；
（3）如图2，已知：△ABC中，∠B是锐角，ctan C=2，AB=10，BC=20，试求∠B的余弦cosB的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图为长方形纸带，AD平行BC，E、F分别是边AD、BC上一点，∠DEF＝α，α为锐角且α≠60°，将纸带沿EF折叠如图（1），再由GF折叠如图（2），若GP平分∠MGF交直线EF于点P，则∠GPE＝_____（含α的式子表示）
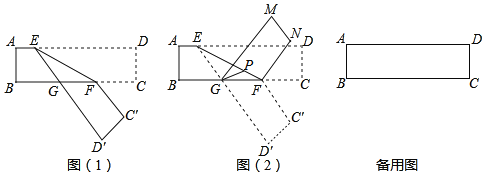
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．
（1）求证：四边形ABCD是菱形；
（2）如果BE=BC，且∠CBE：∠BCE=2：3，求证：四边形ABCD是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了奖励在数学竞赛中获奖的学生，买了若干本课外读物准备送给他们，如果每人送3本，则剩余8本；如果前面每人送5本，则最后一人得到的课外读物不足3本，设该校买了m本课外读物，有
x名学生获奖，请解答下列问题：
（1）用含x的代数式表示m；
（2）求出该校的获奖人数及所买课外读物的本数.
查看答案和解析>>
科目：初中数学 来源： 题型：
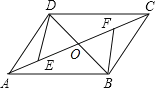
【题目】如图，ABCD的对角线AC，BD相交于点O．E，F是AC上的两点，并且AE=CF，连接DE，BF．
（1）求证：△DOE≌△BOF；
（2）若BD=EF，连接DE，BF．判断四边形EBFD的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知x1，x2，x3，x2019都是不等于0的有理数，若
，求y1的值．
当x1＞0时，
；当x1＜0时，
，所以y1=±1，值有两个．
（1）若
，求y2的值为 ；
（2）若
，则y3的值为 ；
（3）由以上探究猜想，
共有 个不同的值，在y2019这些不同的值中，最大的值和最小的值的差等于 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
