
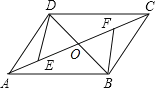
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过![]() 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍![]() ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量![]() 与药物在空气中的持续时间
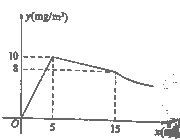
与药物在空气中的持续时间![]() 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
A. 经过![]() 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到![]()
B. 室内空气中的含药量不低于![]() 的持续时间达到了
的持续时间达到了![]()
C. 当室内空气中的含药量不低于![]() 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D. 当室内空气中的含药量低于![]() 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到![]() 开始,需经过
开始,需经过![]() 后,学生才能进入室内
后,学生才能进入室内
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l1的函数关系式为y=2x+b,直线l2过原点且与直线l1交于点P(-1,-5).
(1)试问(-1,-5)可以看作是怎样的二元一次方程组的解?
(2)设直线l1与直线y=x交于点A,求△APO的面积;
(3)在x轴上是否存在点Q,使得△AOQ是等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象交于点(2,1).
的图象与一次函数y=kx+m的图象交于点(2,1).
(1)分别求出这两个函数的解析式;
(2)判断P(﹣1,﹣5)是否在一次函数y=kx+m的图象上,并说明原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛,其预赛成绩如图:
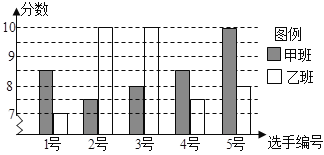
(1)根据上图求出下表中的a,b,c的值(单位:分);
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
(2)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛,求这5人预赛成绩的平均分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
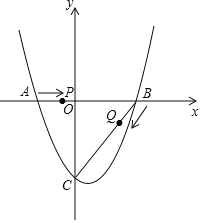
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
x﹣4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P从A点出发,在线段AB上以每秒2个单位长度的速度向B点运动,同时,点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t秒,求运动时间t为多少秒时,△PBQ的面积S最大,并求出其最大面积;
(3)在(2)的条件下,当△PBQ面积最大时,在BC下方的抛物线上是否存在点M,使△BMC的面积是△PBQ面积的1.6倍?若存在,求点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com