
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
x﹣4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
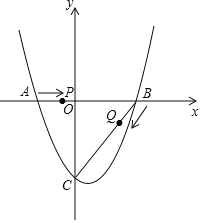
(2)点P从A点出发,在线段AB上以每秒2个单位长度的速度向B点运动,同时,点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t秒,求运动时间t为多少秒时,△PBQ的面积S最大,并求出其最大面积;
(3)在(2)的条件下,当△PBQ面积最大时,在BC下方的抛物线上是否存在点M,使△BMC的面积是△PBQ面积的1.6倍?若存在,求点M的坐标;若不存在,请说明理由.
【答案】(1)点A的坐标为(﹣2,0),点B的坐标为(3,0),点C的坐标为(0,﹣4);(2)当t=![]() 时,△PBQ的面积取最大值,最大值为
时,△PBQ的面积取最大值,最大值为![]() ;(3)点M的坐标为(1,﹣4)或(2,﹣
;(3)点M的坐标为(1,﹣4)或(2,﹣![]() ).
).
【解析】(1)代入x=0可求出点C的纵坐标,代入y=0可求出点A、B的横坐标,此题得解;
(2)根据点B、C的坐标,利用待定系数法可求出直线BC的解析式,过点Q作QE∥y轴,交x轴于点E,当运动时间为t秒时,点P的坐标为(2t-2,0),点Q的坐标为(3-![]() t,-
t,-![]() t),进而可得出PB、QE的长度,利用三角形的面积公式可得出S△PBQ关于t的函数关系式,利用二次函数的性质即可解决最值问题;
t),进而可得出PB、QE的长度,利用三角形的面积公式可得出S△PBQ关于t的函数关系式,利用二次函数的性质即可解决最值问题;
(3)根据(2)的结论找出点P、Q的坐标,假设存在,设点M的坐标为(m,![]() m2-
m2-![]() m-4),则点F的坐标为(m,
m-4),则点F的坐标为(m,![]() m-4),进而可得出MF的长度,利用三角形的面积结合△BMC的面积是△PBQ面积的1.6倍,可得出关于m的一元二次方程,解之即可得出结论.
m-4),进而可得出MF的长度,利用三角形的面积结合△BMC的面积是△PBQ面积的1.6倍,可得出关于m的一元二次方程,解之即可得出结论.
(1)当x=0时,y=![]() x2﹣
x2﹣![]() x﹣4=﹣4,
x﹣4=﹣4,
∴点C的坐标为(0,﹣4);
当y=0时,有![]() x2﹣
x2﹣![]() x﹣4=0,
x﹣4=0,
解得:x1=﹣2,x2=3,
∴点A的坐标为(﹣2,0),点B的坐标为(3,0).
(2)设直线BC的解析式为y=kx+b(k≠0),
将B(3,0)、C(0,﹣4)代入y=kx+b,
![]() ,解得:
,解得: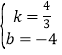 ,
,
∴直线BC的解析式为y=![]() x﹣4.
x﹣4.
过点Q作QE∥y轴,交x轴于点E,如图1所示,
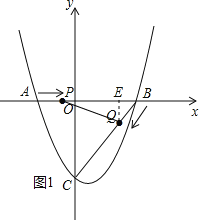
当运动时间为t秒时,点P的坐标为(2t﹣2,0),点Q的坐标为(3﹣![]() t,﹣
t,﹣![]() t),
t),
∴PB=3﹣(2t﹣2)=5﹣2t,QE=![]() t,
t,
∴S△PBQ=![]() PBQE=﹣
PBQE=﹣![]() t2+2t=﹣
t2+2t=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() .
.
∵﹣![]() <0,
<0,
∴当t=![]() 时,△PBQ的面积取最大值,最大值为
时,△PBQ的面积取最大值,最大值为![]() .
.
(3)当△PBQ面积最大时,t=![]() ,
,
此时点P的坐标为(![]() ,0),点Q的坐标为(
,0),点Q的坐标为(![]() ,﹣1).
,﹣1).
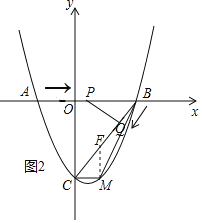
假设存在,设点M的坐标为(m,![]() m2﹣
m2﹣![]() m﹣4),则点F的坐标为(m,
m﹣4),则点F的坐标为(m,![]() m﹣4),
m﹣4),
∴MF=![]() m﹣4﹣(
m﹣4﹣(![]() m2﹣
m2﹣![]() m﹣4)=﹣
m﹣4)=﹣![]() m2+2m,
m2+2m,
∴S△BMC=![]() MFOB=﹣m2+3m.
MFOB=﹣m2+3m.
∵△BMC的面积是△PBQ面积的1.6倍,
∴﹣m2+3m=![]() ×1.6,即m2﹣3m+2=0,
×1.6,即m2﹣3m+2=0,
解得:m1=1,m2=2.
∵0<m<3,
∴在BC下方的抛物线上存在点M,使△BMC的面积是△PBQ面积的1.6倍,点M的坐标为(1,﹣4)或(2,﹣![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
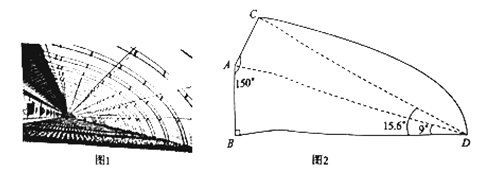
【题目】随着我市农产品整体品牌形象“聊·胜一筹!”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图1.线段![]() ,
,![]() 分别表示大棚的墙高和跨度,
分别表示大棚的墙高和跨度,![]() 表示保温板的长.已知墙高
表示保温板的长.已知墙高![]() 为2米,墙面与保温板所成的角
为2米,墙面与保温板所成的角![]() ,在点
,在点![]() 处测得
处测得![]() 点、
点、![]() 点的仰角分别为
点的仰角分别为![]() ,
,![]() ,如图2.求保温板
,如图2.求保温板![]() 的长是多少米?(精确到0.1米)
的长是多少米?(精确到0.1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
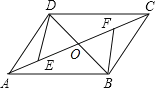
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,过顶点A的直线DE∥BC,∠ABC、∠ACB的平分线分别交DE于点E、D,若AC=3,AB=4,则DE的长为( )

A. 6B. 7C. 8D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五一期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:

(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为1的正方形纸片分割成7个部分,第①部分是边长不1的正方形纸片面积的一半,第②部分是第①部分面积的半,第③部分是第③部分面积的一半,…,依次类推.
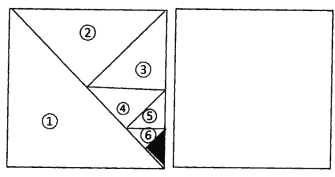
(1)阴影部分的面积是多少?
(2)受此启发,你能求出![]() 的值吗?
的值吗?
(3)请你利用图中右侧的正方形,再设计能求![]() 的值的几何图形.(只画出图形即可)
的值的几何图形.(只画出图形即可)
(4)根据以上规律,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
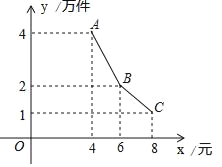
【题目】为了支持大学生创业,某市政府出台了一项优惠政策:提供10万元的无息创业贷款.小王利用这笔贷款,注册了一家淘宝网店,招收5名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款.已知该产品的成本为每件4元,员工每人每月的工资为4千元,该网店还需每月支付其它费用1万元.该产品每月销售量y(万件)与销售单价x(元)万件之间的函数关系如图所示.
(1)求该网店每月利润w(万元)与销售单价x(元)之间的函数表达式;
(2)小王自网店开业起,最快在第几个月可还清10万元的无息贷款?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com