
【题目】已知x1,x2,x3,x2019都是不等于0的有理数,若![]() ,求y1的值.
,求y1的值.
当x1>0时,![]() ;当x1<0时,
;当x1<0时,![]() ,所以y1=±1,值有两个.
,所以y1=±1,值有两个.
(1)若![]() ,求y2的值为 ;
,求y2的值为 ;
(2)若![]() ,则y3的值为 ;
,则y3的值为 ;
(3)由以上探究猜想,![]() 共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
【答案】(1)![]() 或0;(2)±1或±3;(3)2020,4038.
或0;(2)±1或±3;(3)2020,4038.
【解析】
(1)由题意可得![]() ,以此进行代入计算即可求得答案;
,以此进行代入计算即可求得答案;
(2)根据题意可得![]() ,
,![]() ,并将其值代入式子分类讨论进行计算即可;
,并将其值代入式子分类讨论进行计算即可;
(3)根据题意由(1)(2)可知,y1有两个值,y2有三个值,y3有四个值,…,
由此规律可知,y2019有2020个值,以此进行分析得出最大的值和最小的值的差.
解:(1)∵由题意可得![]() ,
,
∴![]() 或0.
或0.
故答案为:![]() 或0.
或0.
(2)∵由题意可得![]() ,
,![]() ,
,
∴![]() ±1或±3.
±1或±3.
故答案为:±1或±3.
(3)由(1)(2)可知,y1有两个值,y2有三个值,y3有四个值,…,
由此规律可知,y2019有2020个值,
最大值为2019个1相加即为2019,最小值为2019个-1相加即为-2019,
最大值与最小值的差为2019-(-2019)=4038.
故答案为:2020,4038.


科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象交于点(2,1).
的图象与一次函数y=kx+m的图象交于点(2,1).
(1)分别求出这两个函数的解析式;
(2)判断P(﹣1,﹣5)是否在一次函数y=kx+m的图象上,并说明原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
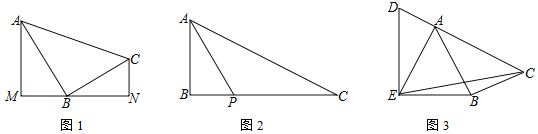
【题目】在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=![]() ,求tanC的值;
,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=![]() ,
,![]() ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
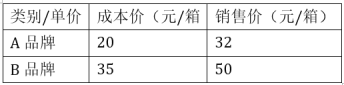
【题目】列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
(1)该大型超市购进A、B品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,CD是△ACB的角平分线.若在边AC上截取CE=CB,连接DE,则图中等腰三角形共有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件是( )

A. AD=BC
B. AC=BD
C. AB=CD
D. AD=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
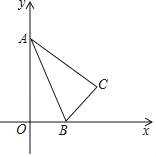
【题目】如图,Rt△ABC中,BC=4,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
(1)AB中点P经过的路径长_____.
(2)点C运动的路径长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com