
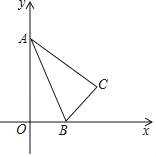
【题目】如图,Rt△ABC中,BC=4,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
(1)AB中点P经过的路径长_____.
(2)点C运动的路径长是_____.
【答案】 ![]() π 8
π 8![]() ﹣12
﹣12
【解析】(1)根据直角三角形斜边中线等于斜边一半,确定中点P的运动路径:以O为圆心,以OP为半径的![]() 圆弧,半径OP=
圆弧,半径OP=![]() AB=2
AB=2![]() ,代入周长公式计算即可;
,代入周长公式计算即可;
(2)分为两种情况:
①当A从O到现在的点A处时,如图2,此时C′A⊥y轴,点C运动的路径长是CC′的长;
②当A再继续向上移动,直到点B与O重合时,如图3,此时点C运动的路径是从C′到C,长是CC′;
分别计算并相加.
(1)如图1.
∵∠AOB=90°,P为AB的中点,∴OP=![]() AB.
AB.
∵AB=4![]() ,∴OP=2
,∴OP=2![]() ,∴AB中点P运动的轨迹是以O为圆心,以OP为半径的
,∴AB中点P运动的轨迹是以O为圆心,以OP为半径的![]() 圆弧,即AB中点P经过的路径长=
圆弧,即AB中点P经过的路径长=![]() ×2×2
×2×2![]() π=
π=![]() π;
π;
(2)①当A从O到现在的点A处时,如图2,此时C′A⊥y轴,点C运动的路径长是CC′的长,∴AC′=OC=8.
∵AC′∥OB,∴∠AC′O=∠COB,∴cos∠AC′O=cos∠COB=![]() =
=![]() =
=![]() ,∴OC′=4
,∴OC′=4![]() ,∴CC′=4
,∴CC′=4![]() ﹣8;
﹣8;
②当A再继续向上移动,直到点B与O重合时,如图3,此时点C运动的路径是从C′到C,长是CC′,CC′=OC′﹣BC=4![]() ﹣4.
﹣4.
综上所述:点C运动的路径长是:4![]() ﹣8+4
﹣8+4![]() ﹣4=8
﹣4=8![]() ﹣12;
﹣12;
故答案为:(1)![]() π; (2)8
π; (2)8![]() ﹣12.
﹣12.



 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知x1,x2,x3,x2019都是不等于0的有理数,若![]() ,求y1的值.
,求y1的值.
当x1>0时,![]() ;当x1<0时,
;当x1<0时,![]() ,所以y1=±1,值有两个.
,所以y1=±1,值有两个.
(1)若![]() ,求y2的值为 ;
,求y2的值为 ;
(2)若![]() ,则y3的值为 ;
,则y3的值为 ;
(3)由以上探究猜想,![]() 共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数百位上数字是![]() ,十位上数字是
,十位上数字是![]() .个位上数字是
.个位上数字是![]() ,则这个三位数可记作
,则这个三位数可记作![]()
(1)若一个两位数![]() .满足关系式
.满足关系式![]() .
.
①试求出![]() 的数量关系:
的数量关系:
②请直接写出满足关系式![]() 的所有两位数.
的所有两位数.
(2)将一个三位数![]() ,其中
,其中![]() .现将三位数
.现将三位数![]() 中间数字
中间数字![]() 去掉,成为一个两位数
去掉,成为一个两位数![]() 且满足
且满足![]() .请直接写出所有符合条件的三位数.
.请直接写出所有符合条件的三位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
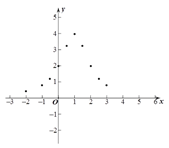
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连结DE,EF.
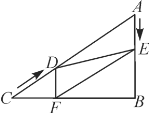
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(2)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若任意一个代数式,在给定的范围内求得的最值恰好也在该范围内,则称这个代数式是这个范围的“友好代数式”.例如:关于![]() 的代数式
的代数式![]() ,当
,当![]() 时,代数式
时,代数式![]() 在
在![]() 时有最大值,最大值为1;在
时有最大值,最大值为1;在![]() 时有最小值,最小值为0,此时最值1,0均在
时有最小值,最小值为0,此时最值1,0均在![]() (含端点)这个范围内,则称代数式
(含端点)这个范围内,则称代数式![]() 是
是![]() 的“友好代数式”.
的“友好代数式”.
(1)若关于![]() 的代数式
的代数式![]() ,当
,当![]() 时,取得的最大值为________;最小值为________;代数式
时,取得的最大值为________;最小值为________;代数式![]() ________(填“是”或“不是”)
________(填“是”或“不是”)![]() 的“友好代数式”;
的“友好代数式”;
(2)以下关于![]() 的代数式,是
的代数式,是![]() 的“友好代数式”的是________;
的“友好代数式”的是________;
①![]() ;②
;②![]() ;③
;③![]() ;
;
(3)若关于![]() 的代数式
的代数式![]() 是
是![]() 的“友好代数式”,则
的“友好代数式”,则![]() 的值是________;
的值是________;
(4)若关于![]() 的代数式
的代数式![]() 是
是![]() 的“友好代数式”,求
的“友好代数式”,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
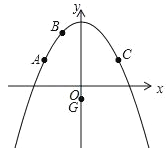
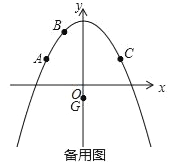
【题目】二次函数y=ax2+c的图象经过点A(﹣4,3),B(﹣2,6),点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点G(0,﹣1).
(1)求出点C坐标及抛物线的解析式;
(2)若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
(3)若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将△QGM沿QG翻折得到△QGN,当点N在坐标轴上时,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有4个红球,3个白球,2个黄球,每个球除颜色外都相同.
(1)请判断下列事件是不确定事件、不可能事件还是必然事件,填写在横线上.
①从口袋中任意摸出1个球是白球;
②从口袋中任意摸出4个球全是白球;
③从口袋中任意摸出1个球是红球或黄球;
④从口袋中任意摸出8个球,红、白、黄三种颜色的球都有;
(2)请求出(1)中不确定事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
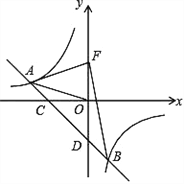
【题目】如图,一次函数 yax 2(a0) 的图象与反比例函数 y![]() (k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=
(k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=![]() ,AO=
,AO=![]() .
.
(1)求这个一次函数和反比例函数的解析式;
(2) 若点 F 是点D 关于 x 轴的对称点,求△ABF 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com