
°æƒø°ø»Ù»Œ“‚“ª∏ˆ¥˙ ˝ Ω£¨‘⁄∏¯∂®µƒ∑∂Œßƒ⁄«Ûµ√µƒ◊Ó÷µ«°∫√“≤‘⁄∏√∑∂Œßƒ⁄£¨‘Ú≥∆’‚∏ˆ¥˙ ˝ Ω «’‚∏ˆ∑∂Œßµƒ°∞”—∫√¥˙ ˝ Ω°±£Æ¿˝»Á£∫πÿ”⁄![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() £¨µ±
£¨µ±![]() ±£¨¥˙ ˝ Ω
±£¨¥˙ ˝ Ω![]() ‘⁄
‘⁄![]() ±”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™1£ª‘⁄
±”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™1£ª‘⁄![]() ±”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™0£¨¥À ±◊Ó÷µ1£¨0æ˘‘⁄
±”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™0£¨¥À ±◊Ó÷µ1£¨0æ˘‘⁄![]() £®∫¨∂Àµ„£©’‚∏ˆ∑∂Œßƒ⁄£¨‘Ú≥∆¥˙ ˝ Ω
£®∫¨∂Àµ„£©’‚∏ˆ∑∂Œßƒ⁄£¨‘Ú≥∆¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
£®1£©»Ùπÿ”⁄![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() £¨µ±
£¨µ±![]() ±£¨»°µ√µƒ◊Ó¥Û÷µŒ™________£ª◊Ó–°÷µŒ™________£ª¥˙ ˝ Ω
±£¨»°µ√µƒ◊Ó¥Û÷µŒ™________£ª◊Ó–°÷µŒ™________£ª¥˙ ˝ Ω![]() ________£®ÃÓ°∞ «°±ªÚ°∞≤ª «°±£©
________£®ÃÓ°∞ «°±ªÚ°∞≤ª «°±£©![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£ª
µƒ°∞”—∫√¥˙ ˝ Ω°±£ª
£®2£©“‘œ¬πÿ”⁄![]() µƒ¥˙ ˝ Ω£¨ «
µƒ¥˙ ˝ Ω£¨ «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±µƒ «________£ª
µƒ°∞”—∫√¥˙ ˝ Ω°±µƒ «________£ª
¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() £ª
£ª
£®3£©»Ùπÿ”⁄![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£¨‘Ú
µƒ°∞”—∫√¥˙ ˝ Ω°±£¨‘Ú![]() µƒ÷µ «________£ª
µƒ÷µ «________£ª
£®4£©»Ùπÿ”⁄![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£¨«Û
µƒ°∞”—∫√¥˙ ˝ Ω°±£¨«Û![]() µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
°æ¥∞∏°ø£®1£©3£¨0£¨≤ª « £®2£©¢⁄ £®3£©![]() £®4£©
£®4£©![]() µƒ◊Ó¥Û÷µŒ™4∫Õ◊Ó–°÷µŒ™0£Æ
µƒ◊Ó¥Û÷µŒ™4∫Õ◊Ó–°÷µŒ™0£Æ
°æΩ‚Œˆ°ø
£®1£©«Û≥ˆ¥˙ ˝ Ωµƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£¨‘Ÿ∏˘æð”—∫√¥˙ ˝ Ωµƒ∂®“ÂΩ¯––≈–∂œº¥ø…£ª
£®2£©∏˘æð”—∫√¥˙ ˝ Ωµƒ∂®“Â∂‘∏˜¥˙ ˝ ΩΩ¯––«ÛΩ‚º¥ø…£ª
£®3£©∑÷»˝÷÷«ÈøˆΩ¯––«ÛΩ‚£∫¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() £¨º¥ø…«Û≥ˆmµƒ÷µ£ª
£¨º¥ø…«Û≥ˆmµƒ÷µ£ª
£®4£©∑÷»˝÷÷«ÈøˆΩ¯––«ÛΩ‚£∫¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨º¥ø…«Û≥ˆ
£¨º¥ø…«Û≥ˆ![]() µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
£®1£©°þ![]()
°ýµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™3£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™3£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™0
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™0
°ý![]() £¨
£¨![]()
π ¥˙ ˝ Ω![]() ≤ª «
≤ª «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
£®2£©¢Ÿ°þµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™3£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™3£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-1£¨
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-1£¨
°ý![]() £¨
£¨![]()
°ý![]() ≤ª «
≤ª «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
¢⁄°þµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™2£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™2£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-2£¨
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-2£¨
°ý![]() £¨
£¨![]()
°ý![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
¢€°þµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™2£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™2£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-4£¨
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-4£¨
°ý![]() £¨
£¨![]()
°ý![]() ≤ª «
≤ª «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
π «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±µƒ «¢⁄£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±µƒ «¢⁄£Æ
£®3£©°þπÿ”⁄![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±
µƒ°∞”—∫√¥˙ ˝ Ω°±
°ý∑÷“‘œ¬»˝÷÷«ÈøˆΩ¯––Ã÷¬€£∫
¢Ÿ![]()
![]()
°ýµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™4£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™4£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™![]() £¨
£¨
°ý![]()
°ý≤ª≥…¡¢
¢⁄![]()
![]()
°ý![]() £¨
£¨![]()
°ý![]()
Ω‚µ√![]()
°ýµ±![]() ≥…¡¢
≥…¡¢
¢€![]()
![]()
°ýµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-4£¨
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-4£¨
°þ![]()
°ý≤ª≥…¡¢
π ![]() µƒ÷µ «
µƒ÷µ «![]() £Æ
£Æ
£®4£©°þπÿ”⁄![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±
µƒ°∞”—∫√¥˙ ˝ Ω°±
°ý∑÷“‘œ¬»˝÷÷«ÈøˆΩ¯––Ã÷¬€
¢Ÿ![]()
µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™![]() £¨
£¨
°ý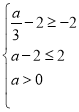
Ω‚µ√![]()
¢⁄![]()
![]()
°þ![]()
°ý![]() ±≥…¡¢
±≥…¡¢
¢€![]()
µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™![]() £¨
£¨
°ý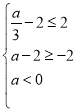
ŒÞΩ‚
°ý![]()
°ý![]() µƒ◊Ó¥Û÷µŒ™4∫Õ◊Ó–°÷µŒ™0£Æ
µƒ◊Ó¥Û÷µŒ™4∫Õ◊Ó–°÷µŒ™0£Æ


 øº«∞±ÿ¡∑œµ¡–¥∞∏
øº«∞±ÿ¡∑œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨°œA=36°„£¨AB=AC£¨CD «°˜ACBµƒΩ«∆Ω∑÷œþ£Æ»Ù‘⁄±þAC…œΩÿ»°CE=CB£¨¡¨Ω”DE£¨‘ÚÕº÷–µ»—¸»˝Ω«–Œπ≤”–£®°°°°£©

A. 2∏ˆB. 3∏ˆC. 4∏ˆD. 5∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œC£Ω90°„£¨AC£ΩBC£Ω10cm£¨µ„P¥”µ„B≥ˆ∑¢£¨—ÿBA∑ΩœÚ“‘√ø√Î![]() cmµƒÀŸ∂»œÚ÷’µ„A‘À∂Ø£ªÕ¨ ±£¨∂ص„Q¥”µ„C≥ˆ∑¢—ÿCB∑ΩœÚ“‘√ø√Î1 cmµƒÀŸ∂»œÚ÷’µ„B‘À∂Ø£¨Ω´°˜BPQ—ÿBC∑≠’€£¨µ„Pµƒ∂‘”¶µ„Œ™µ„P°‰£¨…ËQµ„‘À∂صƒ ±º‰Œ™t√Σ¨µ±Àƒ±þ–ŒQPBP°‰Œ™¡‚–Œ ±£¨tµƒ÷µŒ™____£Æ
cmµƒÀŸ∂»œÚ÷’µ„A‘À∂Ø£ªÕ¨ ±£¨∂ص„Q¥”µ„C≥ˆ∑¢—ÿCB∑ΩœÚ“‘√ø√Î1 cmµƒÀŸ∂»œÚ÷’µ„B‘À∂Ø£¨Ω´°˜BPQ—ÿBC∑≠’€£¨µ„Pµƒ∂‘”¶µ„Œ™µ„P°‰£¨…ËQµ„‘À∂صƒ ±º‰Œ™t√Σ¨µ±Àƒ±þ–ŒQPBP°‰Œ™¡‚–Œ ±£¨tµƒ÷µŒ™____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°˜ABC÷–£¨°œBAC=60°„£¨AB=AC£¨µ„DŒ™÷±œþBC…œ“ª∂ص„£®µ„D≤ª”ÎB£¨C÷ÿ∫œ£©£¨“‘ADŒ™±þ‘⁄AD”“≤ý◊˜¡‚–ŒADEF£¨ π°œDAF=60°„£¨¡¨Ω”CF£Æ
£®1£©π€≤Ï≤¬œÎ£∫»ÁÕº1£¨µ±µ„D‘⁄œþ∂ŒBC…œ ±£¨¢ŸAB”ÎCFµƒŒª÷√πÿœµŒ™£∫°° °°£ª
¢⁄BC£¨CD£¨CF÷ƺ‰µƒ ˝¡øπÿœµŒ™£∫°° °°£Æ
£®2£© ˝—ßÀºøº£∫»ÁÕº2£¨µ±µ„D‘⁄œþ∂ŒCBµƒ—”≥§œþ…œ ±£¨Ω·¬€¢Ÿ£¨¢⁄ «∑Ò»‘»ª≥…¡¢£ø»Ù≥…¡¢£¨«Î∏¯”Ë÷§√˜£ª»Ù≤ª≥…¡¢£¨«Îƒ„–¥≥ˆ’˝»∑Ω·¬€‘Ÿ∏¯”Ë÷§√˜£Æ
£®3£©Õÿ’π—”…Ï£∫»ÁÕº3£¨µ±µ„D‘⁄œþ∂ŒBCµƒ—”≥§œþ…œ ±£¨…ËAD”ÎCFœýΩª”⁄µ„G£¨»Ù“—÷™AB=4£¨CD=![]() AB£¨«ÛAGµƒ≥§£Æ
AB£¨«ÛAGµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
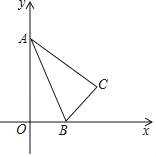
°æƒø°ø»ÁÕº£¨Rt°˜ABC÷–£¨BC=4£¨AC=8£¨Rt°˜ABCµƒ–±±þ‘⁄x÷·µƒ’˝∞Î÷·…œ£¨µ„A”Α≠µ„÷ÿ∫œ£¨ÀÊ◊≈∂•µ„A”…Oµ„≥ˆ∑¢—ÿy÷·µƒ’˝∞Î÷·∑ΩœÚª¨∂Ø£¨µ„B“≤—ÿ◊≈x÷·œÚµ„Oª¨∂Ø£¨÷±µΩ”ε„O÷ÿ∫œ ±‘À∂ØΩ· ¯£Æ‘⁄’‚∏ˆ‘À∂Øπ˝≥Ã÷–£Æ
£®1£©AB÷–µ„Pæ≠π˝µƒ¬∑æ∂≥§_____£Æ
£®2£©µ„C‘À∂صƒ¬∑æ∂≥§ «_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÃΩæø
(1)“—÷™»ÁÕº1£¨»ÙAB°ŒCD£¨PŒ™∆Ω––œþƒ⁄µƒ“ªµ„«Îƒ„≈–∂œ°œB+°œP+°œD= ∂»£¨≤¢Àµ√˜¿Ì”….
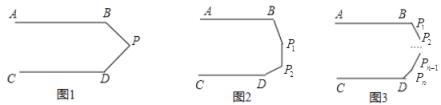
(2)»ÁÕº2£¨»ÙAB°ŒCD £¨P1°¢P2Œ™∆Ω––œþƒ⁄µƒ¡Ω∏ˆµ„£¨«Î«Û≥ˆ°œB+°œP1+°œP2+°œD= ∂»(≤ª–Ë“™Àµ√˜¿Ì”…)
(3)»ÁÕº3£¨»Á¥À¿ýÕ∆»ÙAB°ŒCD£¨P1°¢°¢P2°¢P3°¢P4°¢°≠°≠PnŒ™∆Ω––œþƒ⁄µƒn∏ˆµ„£¨«Î«Û≥ˆ°œB+°œP1+°œP2+°œP3+°≠°≠£Æ+°œPn-1+°œPn+°œD= ∂»(≤ª–Ë“™Àµ√˜¿Ì”…)
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£¨“ª¥Œ∫Ø ˝y=£®1-3k£©x+2k-1£¨ ‘ªÿ¥£∫
£®1£©kŒ™∫Œ÷µ ±£¨yÀÊxµƒ‘ˆ¥Û∂¯ºı–°£ø
£®2£©kŒ™∫Œ÷µ ±£¨ÕºœÒ”Îy÷·Ωªµ„‘⁄x÷·…œ∑Ω£ø
£®3£© »Ù“ª¥Œ∫Ø ˝y=£®1-3k£©x+2k-1æ≠π˝µ„£®3£¨4£©£Æ«Î«Û≥ˆ“ª¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø≥««¯ƒ≥–¬Ω®◊°’¨–°«¯º∆ªÆπ∫¬Ú≤¢÷÷÷≤º◊°¢““¡Ω÷÷ ˜√Áπ≤300÷ͣƓ—÷™º◊÷÷ ˜√Á√ø÷Í60‘™£¨““÷÷ ˜√Á√ø÷Í90‘™£Æ
£®1£©»Ùπ∫¬Ú ˜√Áπ≤”√21000‘™£¨Œ º◊°¢““¡Ω÷÷ ˜√Á”¶∏˜¬Ú∂ý…Ÿ÷Í£ø
£®2£©æðÕ≥º∆£¨º◊°¢““¡Ω÷÷ ˜√Á√ø÷Í ˜√Á∂‘ø’∆¯µƒæªªØ÷∏ ˝∑÷±Œ™![]() ∫Õ
∫Õ![]() £¨Œ »Á∫Œπ∫¬Úº◊°¢““¡Ω÷÷ ˜√Á≤≈ƒÐ±£÷§∏√–°«¯µƒø’∆¯æªªØ÷∏ ˝÷Æ∫Õµ»”⁄90£ø
£¨Œ »Á∫Œπ∫¬Úº◊°¢““¡Ω÷÷ ˜√Á≤≈ƒÐ±£÷§∏√–°«¯µƒø’∆¯æªªØ÷∏ ˝÷Æ∫Õµ»”⁄90£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
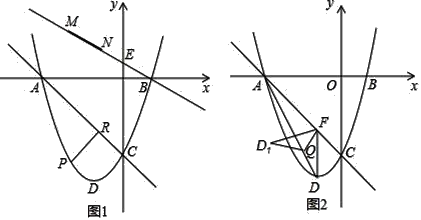
°æƒø°ø»ÁÕº1£¨“—÷™≈◊ŒÔœþy=x2+2x©Å3”Îx÷·œýΩª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨DŒ™∂•µ„£Æ
£®1£©«Û÷±œþACµƒΩ‚Œˆ Ω∫Õ∂•µ„Dµƒ◊¯±Í£ª
£®2£©“—÷™E£®0£¨ ![]() £©£¨µ„P «÷±œþACœ¬∑Ωµƒ≈◊ŒÔœþ…œ“ª∂ص„£¨◊˜PR°ÕAC”⁄µ„R£¨µ±PR◊Ó¥Û ±£¨”–“ªÃı≥§Œ™
£©£¨µ„P «÷±œþACœ¬∑Ωµƒ≈◊ŒÔœþ…œ“ª∂ص„£¨◊˜PR°ÕAC”⁄µ„R£¨µ±PR◊Ó¥Û ±£¨”–“ªÃı≥§Œ™![]() µƒœþ∂ŒMN£®µ„M‘⁄µ„Nµƒ◊Û≤ý£©‘⁄÷±œþBE…œ“∆∂Ø£¨ ◊Œ≤À≥¥Œ¡¨Ω”A°¢M°¢N°¢Pππ≥…Àƒ±þ–ŒAMNP£¨«Î«Û≥ˆÀƒ±þ–ŒAMNPµƒ÷Ð≥§◊Ó–° ±µ„Nµƒ◊¯±Í£ª
µƒœþ∂ŒMN£®µ„M‘⁄µ„Nµƒ◊Û≤ý£©‘⁄÷±œþBE…œ“∆∂Ø£¨ ◊Œ≤À≥¥Œ¡¨Ω”A°¢M°¢N°¢Pππ≥…Àƒ±þ–ŒAMNP£¨«Î«Û≥ˆÀƒ±þ–ŒAMNPµƒ÷Ð≥§◊Ó–° ±µ„Nµƒ◊¯±Í£ª
£®3£©»ÁÕº2£¨π˝µ„D◊˜DF°Œy÷·Ωª÷±œþAC”⁄µ„F£¨¡¨Ω”AD£¨Qµ„ «œþ∂ŒAD…œ“ª∂ص„£¨Ω´°˜DFQ—ÿ÷±œþFQ’€µ˛÷¡°˜D1FQ£¨ «∑ҥʑ⁄µ„Q πµ√°˜D1FQ”ΰ˜AFQ÷ÿµ˛≤ø∑÷µƒÕº–Œ «÷±Ω«»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆAQµƒ≥§£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com