
【题目】探究
(1)已知如图1,若AB∥CD,P为平行线内的一点请你判断∠B+∠P+∠D= 度,并说明理由.
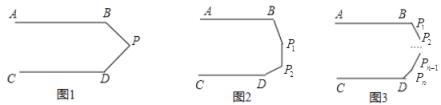
(2)如图2,若AB∥CD ,P1、P2为平行线内的两个点,请求出∠B+∠P1+∠P2+∠D= 度(不需要说明理由)
(3)如图3,如此类推若AB∥CD,P1、、P2、P3、P4、……Pn为平行线内的n个点,请求出∠B+∠P1+∠P2+∠P3+…….+∠Pn-1+∠Pn+∠D= 度(不需要说明理由)
【答案】(1)360°;(2)540°;(3)![]()
【解析】
(1)过点P作AB的平行线PE,利用平行线的性质,即可得到∠B+∠BPD+∠D=180°×2=360°;
(2)过P1作P1F∥AB,过P2作P2G∥CD,则利用平行线的性质,即可得到∠B+∠BP1P2+∠P1P2D+∠D的度数;
(3)利用(1)(2)中的结论,找出规律,即可得到∠A+∠C1+∠C2+……+∠Cn+1+∠D的度数.
解:(1)如图,过点P作AB的平行线PE,
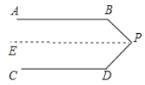
∵AB∥CD,AB∥PE,
∴∠B+∠BPE=180°,∠D+∠DPE=180°,
∵∠BPD=∠BPE+∠DPE,
∴∠B+∠BPD+∠D=180°×2=360°;
故答案为:360°.
(2)如图,过P1作C1F∥AB,过P2作P2G∥DE,
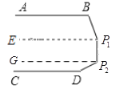
∵AB∥CD,P1F∥AB,过P2作P2G∥CD,
∴∠B+∠BP1F=180°,∠FP1P2+∠P1P2G=180°,∠GP2D+∠D=180°,
∵∠BP1P2=∠BP1F+∠FP1P2,∠P1P2D=∠P1P2G+∠GP2D,
∴∠B+∠BP1P2+∠P1P2D+∠D=180°×3=540°;
故答案为:540°.
(3)由(1)(2)可知,
当B、D两点之间有1个点时,∠B+∠BPD+∠D=180°×2=360°;
当B、D两点之间有2个点时,∠B+∠BP1P2+∠P1P2D+∠D=180°×3=540°;
……
当B、D两点之间有n个点时,有
∠A+∠C1+∠C2+……+∠Cn+1+∠D=180°(n+1);
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过![]() km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方![]() m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为![]() m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD,CD分别是△ABC两个外角的平分线.
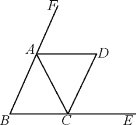
(1)求证:∠ACD=∠ADC;
(2)若∠B=60°,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
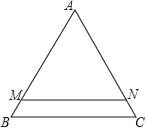
【题目】如图,△ABC中,AB=AC,∠A=60°,BC=6,直线MN∥BC,且分别交边AB,AC于点M,N,已知直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么BD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若任意一个代数式,在给定的范围内求得的最值恰好也在该范围内,则称这个代数式是这个范围的“友好代数式”.例如:关于![]() 的代数式
的代数式![]() ,当
,当![]() 时,代数式
时,代数式![]() 在
在![]() 时有最大值,最大值为1;在
时有最大值,最大值为1;在![]() 时有最小值,最小值为0,此时最值1,0均在
时有最小值,最小值为0,此时最值1,0均在![]() (含端点)这个范围内,则称代数式
(含端点)这个范围内,则称代数式![]() 是
是![]() 的“友好代数式”.
的“友好代数式”.
(1)若关于![]() 的代数式
的代数式![]() ,当
,当![]() 时,取得的最大值为________;最小值为________;代数式
时,取得的最大值为________;最小值为________;代数式![]() ________(填“是”或“不是”)
________(填“是”或“不是”)![]() 的“友好代数式”;
的“友好代数式”;
(2)以下关于![]() 的代数式,是
的代数式,是![]() 的“友好代数式”的是________;
的“友好代数式”的是________;
①![]() ;②
;②![]() ;③
;③![]() ;
;
(3)若关于![]() 的代数式
的代数式![]() 是
是![]() 的“友好代数式”,则
的“友好代数式”,则![]() 的值是________;
的值是________;
(4)若关于![]() 的代数式
的代数式![]() 是
是![]() 的“友好代数式”,求
的“友好代数式”,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
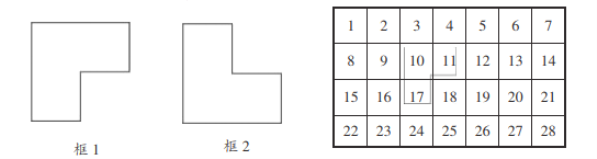
【题目】有两个如图所示的曲尺形框,框![]() 和框
和框![]() ,用它们分别可以框住下表中的三个数(如图所给示例),
,用它们分别可以框住下表中的三个数(如图所给示例),
(1)若被框![]() 框住的三个数中最小的数为
框住的三个数中最小的数为![]() .若这三个数的和是
.若这三个数的和是![]() ,问
,问![]() 的值是否存在?若存在,求出
的值是否存在?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(2)若被框![]() 框住的三个数中最小的数为
框住的三个数中最小的数为![]() .若这三个数的和是
.若这三个数的和是![]() ,问
,问![]() 的值是否存在?若存在,求出
的值是否存在?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
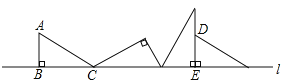
【题目】在Rt△ABC中,AB=1,∠A=60°,∠ABC=90°,如图所示将Rt△ABC沿直线l无滑动地滚动至Rt△DEF,则点B所经过的路径与直线l所围成的封闭图形的面积为_____.(结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
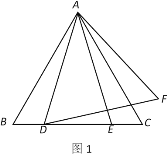
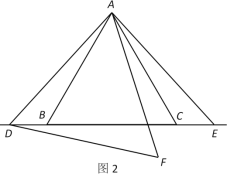
【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE. 点F,点E关于直线AC成轴对称,连接AE,顺次连接A,D,F.
(1)如图1,若点D,点E在边BC上,试判断△ADF的形状并说明理由;
(2)如图2,若点D,点E在边BC外,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
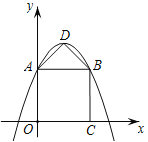
【题目】如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线![]() (a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
(a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com