
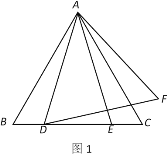
【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE. 点F,点E关于直线AC成轴对称,连接AE,顺次连接A,D,F.
(1)如图1,若点D,点E在边BC上,试判断△ADF的形状并说明理由;
(2)如图2,若点D,点E在边BC外,求证:![]() .
.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
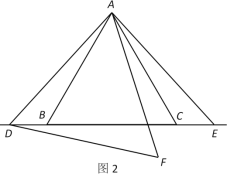
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;
②当AD=25,且AE<DE时,求cos∠PCB的值;
③当BP=9时,求BEEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
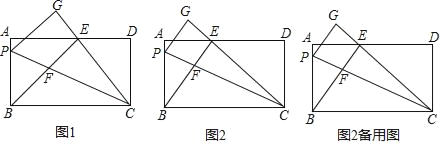
【题目】探究
(1)已知如图1,若AB∥CD,P为平行线内的一点请你判断∠B+∠P+∠D= 度,并说明理由.
(2)如图2,若AB∥CD ,P1、P2为平行线内的两个点,请求出∠B+∠P1+∠P2+∠D= 度(不需要说明理由)
(3)如图3,如此类推若AB∥CD,P1、、P2、P3、P4、……Pn为平行线内的n个点,请求出∠B+∠P1+∠P2+∠P3+…….+∠Pn-1+∠Pn+∠D= 度(不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,已知线段 AB=12 cm,点 C 为线段 AB 上的一动点(点 C 不与 A,B 重合),点D,E 分别是 AC 和 BC 的中点.
(1)若点 C 恰好是 AB 的中点,则 DE= cm;
(2)若 AC=4 cm,求 DE的长;
(3)试说明当点C在线段 AB 上运动时,DE 的长不变;
(4)如图 2,已知∠AOB=120°,在∠AOB 的内部任画一条射线 OC.
①请分别画出∠AOC 和∠COB 的平分线 OD,OE(不要求尺规作图);
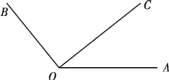
②说明∠DOE 的度数与射线 OC 的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】城区某新建住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.
(1)若购买树苗共用21000元,问甲、乙两种树苗应各买多少株?
(2)据统计,甲、乙两种树苗每株树苗对空气的净化指数分别为![]() 和
和![]() ,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
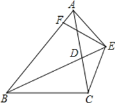
A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有两条边相等的三角形叫做等腰三角形。类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)请你写出一个等对边四边形的名称;
(2)如图,在△ABC中,点D、E分别在AB、AC上,设CD、BE相交于点O,若∠A=50°,![]() .请写出图中其余等于50°的角,并猜想图中哪个四边形为等对边四边形(不需证明);
.请写出图中其余等于50°的角,并猜想图中哪个四边形为等对边四边形(不需证明);
(3)在![]() 中,如果∠A是不等于50°的锐角,点D、E分别在AB、AC上,且
中,如果∠A是不等于50°的锐角,点D、E分别在AB、AC上,且![]() .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
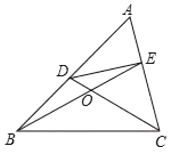
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若![]() ,试求线段CD的长度.
,试求线段CD的长度.
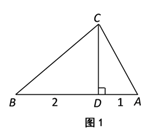
●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
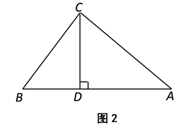
●推广应用
如图3,等腰△ABC为勾股高三角形,其中![]() ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若
,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若![]() ,试求线段DE的长度.
,试求线段DE的长度.
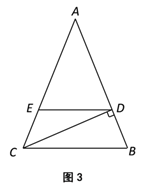
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,AB,CB分别交直线m于点D和点E,且DB=DE,若∠1=65°,则∠BDE的度数为( )
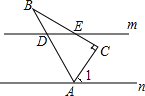
A.115°B.120°C.130°D.145°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com