
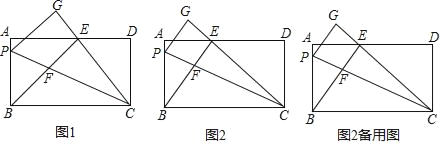
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;
②当AD=25,且AE<DE时,求cos∠PCB的值;
③当BP=9时,求BEEF的值.
【答案】(1)证明见解析;(2)①证明见解析;②![]() ;③108.
;③108.
【解析】(1)先判断出∠A=∠D=90°,AB=DC再判断出AE=DE,即可得出结论;
(2)①利用折叠的性质,得出∠PGC=∠PBC=90°,∠BPC=∠GPC,进而判断出∠GPF=∠PFB即可得出结论;
②判断出△ABE∽△DEC,得出比例式建立方程求解即可得出AE=9,DE=16,再判断出△ECF∽△GCP,进而求出PC,即可得出结论;
③判断出△GEF∽△EAB,即可得出结论.
(1)在矩形ABCD中,∠A=∠D=90°,AB=DC,
∵E是AD中点,
∴AE=DE,
在△ABE和△DCE中,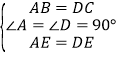 ,
,
∴△ABE≌△DCE(SAS);
(2)①在矩形ABCD,∠ABC=90°,
∵△BPC沿PC折叠得到△GPC,
∴∠PGC=∠PBC=90°,∠BPC=∠GPC,
∵BE⊥CG,
∴BE∥PG,
∴∠GPF=∠PFB,
∴∠BPF=∠BFP,
∴BP=BF;
②当AD=25时,
∵∠BEC=90°,
∴∠AEB+∠CED=90°,
∵∠AEB+∠ABE=90°,
∴∠CED=∠ABE,
∵∠A=∠D=90°,
∴△ABE∽△DEC,
∴![]() ,
,
设AE=x,
∴DE=25﹣x,
∴![]() ,
,
∴x=9或x=16,
∵AE<DE,
∴AE=9,DE=16,
∴CE=20,BE=15,
由折叠得,BP=PG,
∴BP=BF=PG,
∵BE∥PG,
∴△ECF∽△GCP,
∴![]() ,
,
设BP=BF=PG=y,
∴![]() ,
,
∴y=![]() ,
,
∴BP=![]() ,
,
在Rt△PBC中,PC=![]() ,cos∠PCB=
,cos∠PCB=![]() =
=![]() ;
;
③如图,连接FG,
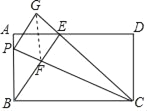
∵∠GEF=∠BAE=90°,
∵BF∥PG,BF=PG,
∴BPGF是菱形,
∴BP∥GF,
∴∠GFE=∠ABE,
∴△GEF∽△EAB,
∴![]() ,
,
∴BEEF=ABGF=12×9=108.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过![]() km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方![]() m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为![]() m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.
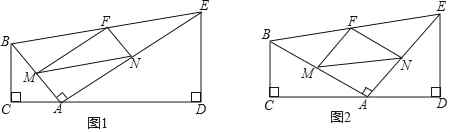
(1)如图②,当BC=4,DE=5,tan∠FMN=1时,求![]() 的值;
的值;
(2)若tan∠FMN=![]() ,BC=4,则可求出图中哪些线段的长?写出解答过程;
,BC=4,则可求出图中哪些线段的长?写出解答过程;
(3)连接CM,DN,CF,DF.试证明△FMC与△DNF全等;
(4)在(3)的条件下,图中还有哪些其它的全等三角形?请直接写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )

A. AE=AFB. EF⊥ACC. ∠B=60°D. AC是∠EAF的平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD,CD分别是△ABC两个外角的平分线.
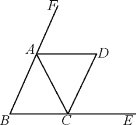
(1)求证:∠ACD=∠ADC;
(2)若∠B=60°,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=60°,BC=6,直线MN∥BC,且分别交边AB,AC于点M,N,已知直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么BD=_____.
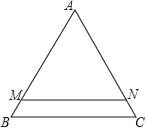
查看答案和解析>>
科目:初中数学 来源: 题型:
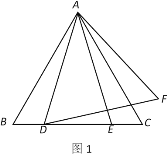
【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE. 点F,点E关于直线AC成轴对称,连接AE,顺次连接A,D,F.
(1)如图1,若点D,点E在边BC上,试判断△ADF的形状并说明理由;
(2)如图2,若点D,点E在边BC外,求证:![]() .
.
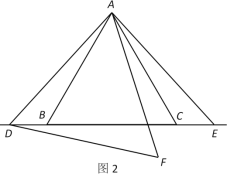
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com