
【题目】如图,在ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )

A. AE=AFB. EF⊥ACC. ∠B=60°D. AC是∠EAF的平分线
【答案】C
【解析】
根据平行四边形性质推出∠B=∠D,∠DAB=∠DCB,AB=CD,AD=BC,求出∠BAE=∠DCF,证△ABE≌△CDF,推出AE=CF,BE=DF,求出AF=CE,得出四边形AECF是平行四边形,再根据菱形的判定判断即可.
解:∵四边形ABCD是平行四边形,
∴∠B=∠D,∠DAB=∠DCB,AB=CD,AD=BC,
∵AE,CF分别是∠BAD和∠BCD的平分线,
∴∠DCF=![]() ∠DCB,∠BAE=
∠DCB,∠BAE=![]() ∠BAD,
∠BAD,
∴∠BAE=∠DCF,
∵在△ABE和△CDF中,∠D=∠B,AB=CD,∠DCF=∠BAE,
∴△ABE≌△CDF,
∴AE=CF,BE=DF,
∵AD=BC,
∴AF=CE,
∴四边形AECF是平行四边形,
A、∵四边形AECF是平行四边形,AE=AF,
∴平行四边形AECF是菱形,故本选项正确;
B、∵EF⊥AC,四边形AECF是平行四边形,
∴平行四边形AECF是菱形,故本选项正确;
C、根据∠B=60°和平行四边形AECF不能推出四边形是菱形,故本选项错误;
D、∵四边形AECF是平行四边形,
∴AF∥BC,
∴∠FAC=∠ACE,
∵AC平分∠EAF,
∴∠FAC=∠EAC,
∴∠EAC=∠ECA,
∴AE=EC,
∵四边形AECF是平行四边形,
∴四边形AECF是菱形,故本选项正确;
故选:C.


科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成2块C型钢板和1块D型钢板;用1块B型钢板可制成1块C型钢板和3块D型钢板.现准备购买A、B型钢板共100块,并全部加工成C、D型钢板.要求C型钢板不少于120块,D型钢板不少于250块,设购买A型钢板x块(x为整数).
(1)求A、B型钢板的购买方案共有多少种?
(2)出售C型钢板每块利润为100元,D型钢板每块利润为120元.若将C、D型钢板全部出售,请你设计获利最大的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一根12米长的木材做一个中间有一条横档的日字形窗户.设AB=x米.
(1)用含有x的代数式表示线段AC的长.
(2)若使透进窗户的光线达到6平方米,则窗户的长和宽各为多少?
(3)透进窗户的光线能达到9平方米吗?若能,请求出这个窗户的长和宽;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
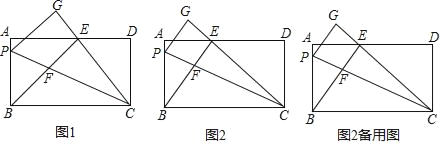
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;
②当AD=25,且AE<DE时,求cos∠PCB的值;
③当BP=9时,求BEEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.

解:∵∠1=∠B
∴AD∥( )(内错角相等,两直线平行)
∴∠C+∠2=180°,( )
∵∠C=110°.
∴∠2=( )°.
∴∠3=∠2=70°.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
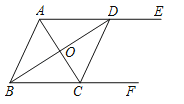
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影《我和我的祖国》讲述了新中国成立70年间普通百姓与共和国息息相关的故事.影片上映15天就斩获票房26亿元人民币,口碑票房实现双丰收.据统计,10月8日,该电影在重庆的票房收入为140万元,接下来7天的票房变化情况如下表(正数表示比前一天增加的票房,负数表示比前一天减少的票房):
日期 | 9日 | 10日 | 11日 | 12日 | 13日 | 14日 | 15日 |
票房变化(万元) |
|
| 0 |
|
|
|
|
(1)这7天中,票房收入最多的是10月________日,票房收入最少的是10月________日;
(2)根据上述数据可知,这7天该电影在重庆的平均票房收入为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
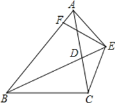
A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com