
【题目】如图①,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.
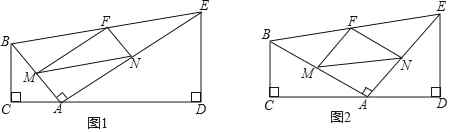
(1)如图②,当BC=4,DE=5,tan∠FMN=1时,求![]() 的值;
的值;
(2)若tan∠FMN=![]() ,BC=4,则可求出图中哪些线段的长?写出解答过程;
,BC=4,则可求出图中哪些线段的长?写出解答过程;
(3)连接CM,DN,CF,DF.试证明△FMC与△DNF全等;
(4)在(3)的条件下,图中还有哪些其它的全等三角形?请直接写出.
【答案】(1)![]() ;(2)可求线段AD的长;(3)证明见解析;(4)△BMF≌△NFM≌△MAN≌△FNE.
;(2)可求线段AD的长;(3)证明见解析;(4)△BMF≌△NFM≌△MAN≌△FNE.
【解析】(1)根据四边形ANFM是平行四边形,AB⊥AE,即可得到四边形ANFM是矩形,再根据FN=FM,即可得出矩形ANFM是正方形,AB=AE,结合∠1=∠3,∠C=∠D=90°,即可得到△ABC≌△EAD,进而得到BC=AD,CA=DE,即可得出![]() ;
;
(2)依据四边形MANF为矩形,MF=![]() AE,NF=
AE,NF=![]() AB,tan∠FMN=
AB,tan∠FMN=![]() ,即可得到
,即可得到![]() =
=![]() ,依据△ABC∽△EAD,即可得到
,依据△ABC∽△EAD,即可得到![]() =
=![]() =
=![]() ,即可得到AD的长;
,即可得到AD的长;
(3)根据△ABC和△ADE都是直角三角形,M,N分别是AB,AE的中点,即可得到BM=CM,NA=ND,进而得出∠4=2∠1,∠5=2∠3,根据∠4=∠5,即可得到∠FMC=∠FND,再根据FM=DN,CM=NF,可得△FMC≌△DNF;
(4)由BM=AM=FN,MF=AN=NE,∠FMB=∠MFN=∠MAN=∠ENF=90°,即可得到:△BMF≌△NFM≌△MAN≌△FNE.
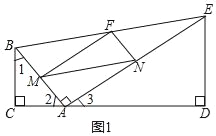
(1)∵点M,N,F分别为AB,AE,BE的中点,
∴MF,NF都是△ABE的中位线,
∴MF=![]() AE=AN,NF=
AE=AN,NF=![]() AB=AM,
AB=AM,
∴四边形ANFM是平行四边形,
又∵AB⊥AE,
∴四边形ANFM是矩形,
又∵tan∠FMN=1,
∴FN=FM,
∴矩形ANFM是正方形,AB=AE,
又∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∵∠C=∠D=90°,
∴△ABC≌△EAD(AAS),
∴BC=AD=4,CA=DE=5,
∴![]() =
=![]() ;
;
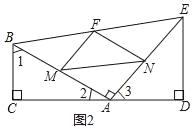
(2)可求线段AD的长.
由(1)可得,四边形MANF为矩形,MF=![]() AE,NF=
AE,NF=![]() AB,
AB,
∵tan∠FMN=![]() ,即
,即![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠1=∠3,∠C=∠D=90°,
∴△ABC∽△EAD,
∴![]() =
=![]() =
=![]() ,
,
∵BC=4,
∴AD=8;
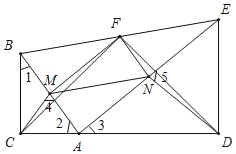
(3)∵BC⊥CD,DE⊥CD,
∴△ABC和△ADE都是直角三角形,
∵M,N分别是AB,AE的中点,
∴BM=CM,NA=ND,
∴∠4=2∠1,∠5=2∠3,
∵∠1=∠3,
∴∠4=∠5,
∵∠FMC=90°+∠4,∠FND=90°+∠5,
∴∠FMC=∠FND,
∵FM=DN,CM=NF,
∴△FMC≌△DNF(SAS);
(4)在(3)的条件下,BM=AM=FN,MF=AN=NE,∠FMB=∠MFN=∠MAN=∠ENF=90°,
∴图中有:△BMF≌△NFM≌△MAN≌△FNE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】先尺规作图,后进行计算:如图,△ABC中,∠A=105°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到∠ABC两边的距离相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=30°,则∠PBC的度数为 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一根12米长的木材做一个中间有一条横档的日字形窗户.设AB=x米.
(1)用含有x的代数式表示线段AC的长.
(2)若使透进窗户的光线达到6平方米,则窗户的长和宽各为多少?
(3)透进窗户的光线能达到9平方米吗?若能,请求出这个窗户的长和宽;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF=![]() +1,求BC的长.
+1,求BC的长.
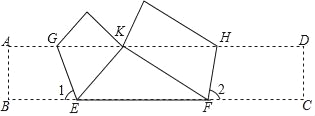
查看答案和解析>>
科目:初中数学 来源: 题型:
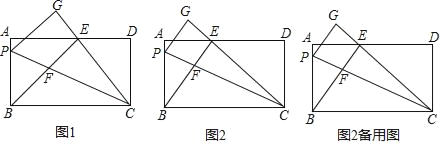
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;
②当AD=25,且AE<DE时,求cos∠PCB的值;
③当BP=9时,求BEEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
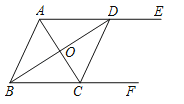
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,已知线段 AB=12 cm,点 C 为线段 AB 上的一动点(点 C 不与 A,B 重合),点D,E 分别是 AC 和 BC 的中点.
(1)若点 C 恰好是 AB 的中点,则 DE= cm;
(2)若 AC=4 cm,求 DE的长;
(3)试说明当点C在线段 AB 上运动时,DE 的长不变;
(4)如图 2,已知∠AOB=120°,在∠AOB 的内部任画一条射线 OC.
①请分别画出∠AOC 和∠COB 的平分线 OD,OE(不要求尺规作图);
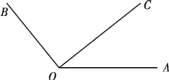
②说明∠DOE 的度数与射线 OC 的位置无关.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com