
����Ŀ���α���չ
��֪���⣺
��������֤���������ε�һ����ǵ������������ڵ������ڽǵĺͣ���ô�������ε�һ���ڽ����������ڵ�������ǵĺ�֮�����������������ϵ�أ�
1������̽����
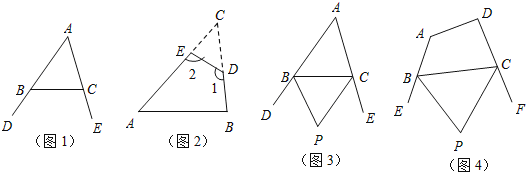
��1����ͼ1����DBC����ECB�ֱ�Ϊ��ABC��������ǣ���̽����A����DBC+��ECB֮�����������������ϵ��Ϊʲô��
2������Ӧ�ã�
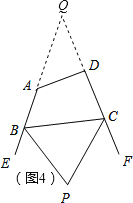
��2����ͼ2������ABCֽƬ�м�ȥ��CED���õ��ı���ABDE����1=130��������2-��C= ��
��3��С�����뵽�����������һ�����⣺��ͼ3������ABC�У�BP��CP�ֱ�ƽ�������DBC����ECB����P����A�к�������ϵ������������Ľ���ֱ��д���� ��
3��չ������
��4����ͼ4�����ı���ABCD�У�BP��CP�ֱ�ƽ�������EBC����FCB����P����A����D�к�������ϵ��Ϊʲô��������Ҫ��������Ľ���˵������ֱ��ʹ�ã�����˵��������
���𰸡���1����DBC+��ECB=180��+��A����2��50������3����P=90��-![]() ��A����4����BAD+��CDA=360��-2��P��
��A����4����BAD+��CDA=360��-2��P��
��������
�����������1�����������ε�һ����ǵ������������ڵ������ڽǵĺͱ�ʾ����DBC+��ECB���������������ڽǺͶ����������ɵý⣻
��2��������1���Ľ����������㼴�ɵý⣻
��3����ʾ����DBC+��ECB���ٸ��ݽ�ƽ���ߵĶ��������PBC+��PCB��Ȼ�������������ڽǺͶ�����ʽ�������ɵý⣻
��4���ӳ�BA��CD�ཻ�ڵ�Q��������Q��ʾ����P��������1���Ľ����������ɵý⣮
�����������1����DBC+��ECB
=180��-��ABC+180��-��ACB
=360��-����ABC+��ACB��
=360��-��180��-��A��
=180��+��A��
��2���ߡ�1+��2=��180��+��C��
��130��+��2=180��+��C��
���2-��C=50����
��3����DBC+��ECB=180��+��A��
��BP��CP�ֱ�ƽ�������DBC����ECB��
���PBC+��PCB=![]() ����DBC+��ECB��=
����DBC+��ECB��=![]() ��180��+��A����
��180��+��A����
����PBC����P=180��-![]() ��180��+��A��=90��-
��180��+��A��=90��-![]() ��A��
��A��
����P=90��-![]() ��A��
��A��
��4���ӳ�BA��CD��Q��
����P=90��-![]() ��Q��
��Q��
���Q=180��-2��P��
���BAD+��CDA=180��+��Q��
=180��+180��-2��P��
=360��-2��P��


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ĵ�����2009��12��15�ն�����2018��10��24����ʽͨ��������������������Ϊ700000ƽ���ף������� 700000 �ÿ�ѧ�������ɱ�ʾ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
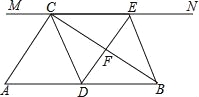
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬����C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE��
��1����֤��CE=AD��
��2����D��AB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��3����DΪAB�е㣬����A�Ĵ�С����ʲô����ʱ���ı���BECD�������Σ���˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ƻ�����4��ѡ�Σ����֡��滭���������赸��ѧУ��ȡ��������ķ��������ʾ����飨ÿ���������ѧ������ѡ�����ֻ��ѡ������һ�ţ����Ե���������ͳ�ƺ��������²�����������ͳ��ͼ��

��������ͳ��ͼ�ṩ����Ϣ���ش��������⣺
��1���˴ε����ȡ��ѧ������Ϊa= �ˣ�����ѡ�滭����ѧ������ռ���������İٷֱ�Ϊb= ��
��2����ȫ����ͳ��ͼ��
��3������У��2000��ѧ���������ȫУѡ�滭����ѧ����Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η���û��ʵ�������ǣ� ��
A.x2��2x��1=0
B.x2+x+3=0
C.x2��1=0
D.x2+2x+1=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ���ֱ����ABC��б��AB��ֱ�DZ�ACΪ������ABC�����ȱ���ABD�͵ȱ���ACE��FΪAB���е㣬DE��AB���ڵ�G��EF��AC���ڵ�H����ACB=90�㣬��BAC=30�㣮�������½��ۣ�
��EF��AC�����ı���ADFEΪ���Σ���AD=4AG����FH=![]() BD��
BD��
������ȷ���۵��ǣ� ��

A���٢ڢ� B���٢ڢ� C���٢ۢ� D���ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
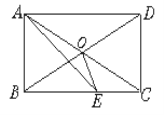
����Ŀ����ͼ���ھ���ABCD�У�AC��BD�ཻ��O��AEƽ�֡�BAD����BC��E������CAE=15�������BOE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���kx2��2x+1��0����������ȵ�ʵ��������k��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�����,�ں���y=2x-6��ͼ���ϵ���( )
A. (-2,3) B. (3,-2) C. (1,4) D. (4,2)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com