

分析 (1)根据正弦函数求得AB、AE的长,进而求得BE的长,即可判定方案是否能保证通行要求;
(2)根据正弦函数和余弦函数求得方案2中的MB的长,即可求得此方案中最多可以停多少辆车;
(3)如图所示新方案,根据车的宽度即可计算出最多停放车辆数.
解答 解:(1)方案1:
如图,AB=2.4×sin45°=2.4×$\frac{\sqrt{2}}{2}$≈1.54米,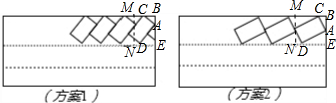
AE=5×sin45°=5×$\frac{\sqrt{2}}{2}$≈3.5米,
BE=AB+AE≈5.04,
∵12-5.04=<7,
∴方案1不能保证通行要求;
方案2:
AB=2.4×cos30°=2.4×$\frac{\sqrt{3}}{2}$≈2.1米,
AE=5×sin30°=5×$\frac{1}{2}$=2.5米,
BE=AB+AE=2.1+2.5=4.6,
∵12-4.6=7.4>7,
∴方案2能保证通行要求;
(2)BC=2.4×sin30°=2.4×$\frac{1}{2}$=1.2米,
MC=5×cos30°=5×$\frac{\sqrt{3}}{2}$≈4.3米,
MB=BC+MC=1.2+4.3=5.5,
60÷5.5=10.9(辆).
故方案2中最多可以停10辆车.
(3)新方案如图: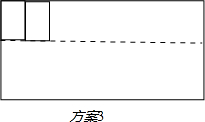
60÷2.4=25(辆).
故这个方案最多可以停放25辆车.
点评 本题考查了学生利用三角函数解决实际问题的能力以及矩形的性质.这就要求学生把实际问题转化为直角三角形的问题,利用三角函数解决问题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
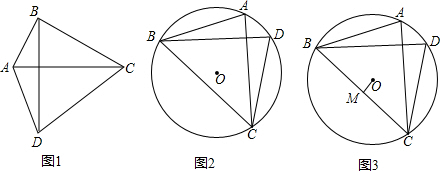
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
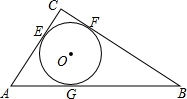 在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com