
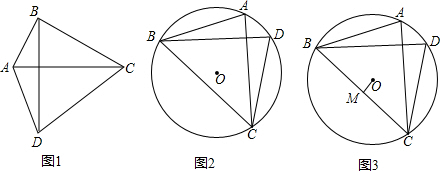
���� ��1�����ݾ��ε����ʺ͡������ı��Ρ��Ķ�������жϣ�
��2������OB��OD����OH��BD��H����ͼ2�����ݴ��������õ�BH=DH������Բ�ܽǶ����õ���BOD=2��BCD=120�㣬�����õ��������ε����ʵá�OBD=30�㣬��Rt��OBH�пɼ����BH=$\sqrt{3}$OH=3$\sqrt{3}$��BD=2BH=6$\sqrt{3}$����AC=BD=6$\sqrt{3}$��Ȼ����������ı��Ρ���������������Խ��߳˻���һ����⣻
��3������OB��OC��OA��OD����OE��AD��E����ͼ3�����ݴ��������õ�AE=DE��������Բ�ܽǶ����õ���BOM=��BAC����AOE=��ABD�������õȽǵ������ȵõ���OBM=��AOE�����֤����BOM�ա�OAE�õ�OM=AE��������OM=$\frac{1}{2}$AD��
���  �⣺��1�����εĶԽ�����ȵ�����ֱ��
�⣺��1�����εĶԽ�����ȵ�����ֱ��
���Ծ��β��ǡ������ı��Ρ���
�ʴ�Ϊ���ǣ�
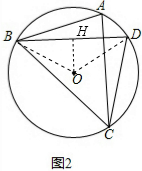
��2������OB��OD����OH��BD��H����ͼ2����BH=DH��
�ߡ�BOD=2��BCD=2��60��=120�㣬
���OBD=30�㣬
��Rt��OBH�У��ߡ�OBH=30�㣬
��OH=$\frac{1}{2}$OB=3��
��BH=$\sqrt{3}$OH=3$\sqrt{3}$��
��BD=2BH=6$\sqrt{3}$��
��AC=BD=6$\sqrt{3}$��
�ࡰ�����ı��Ρ�ABCD�����=$\frac{1}{2}$��6$\sqrt{3}$��6$\sqrt{3}$=54��
��3��OM=$\frac{1}{2}$AD���������£�
����OB��OC��OA��OD����OE��AD��E����ͼ3��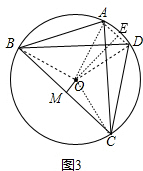
��OE��AD��
��AE=DE��
�ߡ�BOC=2��BAC��
����BOC=2��BOM��
���BOM=��BAC��
ͬ���ɵá�AOE=��ABD��
��BD��AC��
���BAC+��ABD=90�㣬
���BOM+��AOE=90�㣬
�ߡ�BOM+��OBM=90�㣬
���OBM=��AOE��
�ڡ�BOM�͡�OAE��
$\left\{\begin{array}{l}{��BMO=��OEA}\\{��OBM=��AOE}\\{OB=AO}\end{array}\right.$��
���BOM�ա�OAE��
��OM=AE��
��OM=$\frac{1}{2}$AD��
���� ���⿼����Բ���ۺ��⣺��������Բ�ܽǶ������������������������ε����ʺ;��ε����ʣ�������������ȫ�Ƚ���߶���ȵ����⣮


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 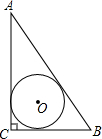 | B�� | 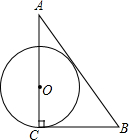 | C�� | 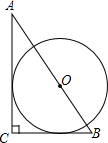 | D�� | 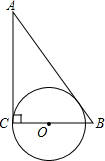 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
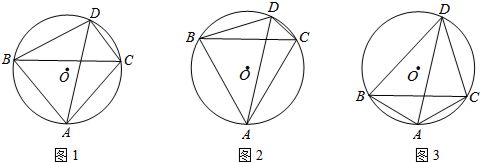
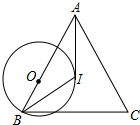 ��ͼ���ڡ�ABC�У�I�ǡ�ABC�����ģ�O��AB����һ�㣬��O����B������AI������I�㣮��tan��BAC=$\frac{24}{7}$����sin��C��ֵΪ��������
��ͼ���ڡ�ABC�У�I�ǡ�ABC�����ģ�O��AB����һ�㣬��O����B������AI������I�㣮��tan��BAC=$\frac{24}{7}$����sin��C��ֵΪ��������| A�� | $\frac{5}{6}$ | B�� | $\frac{4}{5}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com