
| 3 |
 ≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01) 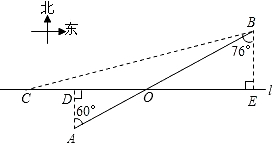 解:(1)设AB与l交于点O.
解:(1)设AB与l交于点O.| AD |
| cos60° |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 12 |
| s |
| t |
| CD | ||
|


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
 于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向.
于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
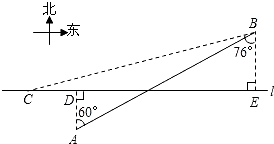
 (2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.
(2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.| 3 |
查看答案和解析>>
科目:初中数学 来源:2012届江西宜春高安市中考二模数学试卷(带解析) 题型:解答题
如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2km,点B位于点A北偏东60°方向且与A相距10km处,现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.
【小题1】求观测点B到航线l的距离;
【小题2】求该轮船航行的速度.(结果精确到0.1km/h)(参考数据, =1.73,sin76°=0.97,cos76°=0.4,tan76°=4.01)
=1.73,sin76°=0.97,cos76°=0.4,tan76°=4.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com