
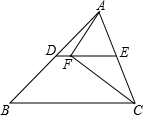
 如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为60°.
如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为60°. 分析 根据三角形的中位线平行于第三边并且等于第三边的一半求出DE∥BC,再根据角平分线的定义求出∠BCF=∠ACF=30°,然后根据平行线的性质求出∠CFE=∠BCF,从而得到∠ACF=∠CFE,再根据等角对等边可得CE=EF,从而求出AE=EF,根据两直线平行,同位角相等可得∠AED=∠ACB=60°,判断出△AEF是等边三角形,最后根据等边三角形的每一个角都是60°解答.
解答 解:∵点D,E分别是AB,AC的中点,
∴DE∥BC,
∵CF恰好平分∠ACB,
∴∠BCF=∠ACF=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,
∵DE∥BC,
∴∠CFE=∠BCF=30°,
∴∠ACF=∠CFE,
∴CE=EF,
∵点E是AC的中点,
∴AE=CE,
∴AE=EF,
∵DE∥BC,
∴∠AED=∠ACB=60°,
∴△AEF是等边三角形,
∴∠FAC=60°.
故答案为:60°.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行线的性质,等边三角形的判定与性质,熟记定理与性质并考虑求出△AEF是等边三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某班同学的身高情况 | B. | 了解全市每天丢弃的废旧电池数 | ||
| C. | 了解50发炮弹的杀伤半径 | D. | 了解我省农民的年人均收入情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查2015年5月份市场上某品牌饮料的质量 | |
| B. | 了解中央电视台某一频道的全国收视率情况 | |
| C. | 环保部门调查2015年5月份黄河某段水域的水质量情况 | |
| D. | 了解全班同学本周末参加社区活动的时间 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 项目/计费方式 | 月租费(元) | 限流量(MB) | 超流量(元/MB) |
| A | 5 | 30 | 0.5 |
| B | 10 | 70 | 1 |
| 流量/计费方式 | t≥30 | 30≤t≤70 | t>70 |
| A种计费(元) | 5 | 0.5t-10 | 0.5t-10 |
| B种计费(元) | 10 | 10 | t-60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
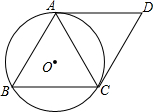 如图,⊙O是△ABC的外接圆,分别过A、C两点作⊙O的两条切线AD、CD,它们的交点为D,且AD∥BC,CD∥AB.
如图,⊙O是△ABC的外接圆,分别过A、C两点作⊙O的两条切线AD、CD,它们的交点为D,且AD∥BC,CD∥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com