
分析 设a=x2-x,则原方程变为a(a-2)=3,求得a的数值,进一步代入求得答案即可.
解答 解:设a=x2-x,则原方程变为a(a-2)=3,
(a+1)(a-3)=0,
解得:a1=-1,a2=3,
当a=-1时,x2-x=-1,
△=1-4=-3<0,此方程无解
当a=3时,x2-x=3,
解得:x1=$\frac{1+\sqrt{13}}{2}$,x2=$\frac{1-\sqrt{13}}{2}$.
所以原方程的解为x1=$\frac{1+\sqrt{13}}{2}$,x2=$\frac{1-\sqrt{13}}{2}$.
故答案为:$\frac{1+\sqrt{13}}{2}$或$\frac{1-\sqrt{13}}{2}$.
点评 此题考查换元法解一元二次方程,用换元法解一元二次方程,注意整体思想的渗透.


科目:初中数学 来源: 题型:解答题
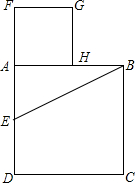 采用如下方法可以得到黄金分割点:如图所示,设AB是已知线段,以AB为边作正方形ABCD;取AD的中点E,连接EB;延长DA至点F,使EF=EB;以线段AF为边作正方形AFGH,点H就是AB的黄金分割点.
采用如下方法可以得到黄金分割点:如图所示,设AB是已知线段,以AB为边作正方形ABCD;取AD的中点E,连接EB;延长DA至点F,使EF=EB;以线段AF为边作正方形AFGH,点H就是AB的黄金分割点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
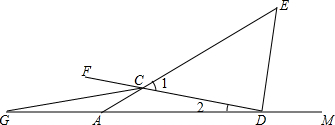 如图,∠CDM,∠FCA为△ACD的二个外角,射线DE、CG分别平分∠CDM、∠FCA,CG交DA的延长线交于点G.∠E=∠1,∠G=∠2,求∠ACD的度数.
如图,∠CDM,∠FCA为△ACD的二个外角,射线DE、CG分别平分∠CDM、∠FCA,CG交DA的延长线交于点G.∠E=∠1,∠G=∠2,求∠ACD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com