
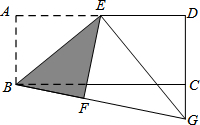
 如图,在矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点F上,连接BF并延长交DC的延长线于点G.
如图,在矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点F上,连接BF并延长交DC的延长线于点G.| 6 |
|
| 6 |


科目:初中数学 来源: 题型:
| 5 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
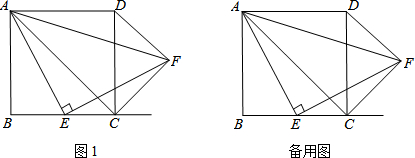
 如图,已知直角三角形ABC,∠C=90°.
如图,已知直角三角形ABC,∠C=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 钓鱼岛及其附属daoyu是我国的固有领土,台湾保diao人士组团前往钓鱼岛,宣示主权.当保diao船航行至海面B处时(如图),测得钓鱼岛位于正北方向20海里的C处,为了防止日本海巡警干扰,就请求我A处的海监船前往C处护航.已知C处位于A处的北偏东45°的方向上,A位于B的北偏西30°的方向上.
钓鱼岛及其附属daoyu是我国的固有领土,台湾保diao人士组团前往钓鱼岛,宣示主权.当保diao船航行至海面B处时(如图),测得钓鱼岛位于正北方向20海里的C处,为了防止日本海巡警干扰,就请求我A处的海监船前往C处护航.已知C处位于A处的北偏东45°的方向上,A位于B的北偏西30°的方向上.| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
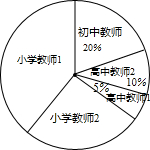 萧山区2014教师招聘有拉开序幕,这给很多有志于教育事业的人员很多机会.下面是今年报考人数统计表(数学)
萧山区2014教师招聘有拉开序幕,这给很多有志于教育事业的人员很多机会.下面是今年报考人数统计表(数学)| 招聘岗位 | 招聘计划 | 报考人数 | |||
| 高中教师1 | 研究生 | 高中 | 数学 | 10 | |
| 高中教师2 | 普通 | 高中 | 数学 | 19 | |
| 初中教师 | 普通 | 初中 | 数学 | 12 | 55 |
| 小学教师1 | 普通 | 城区与八镇 | 数学 | 18 | 83 |
| 小学教师2 | 普通 | 其他 | 数学 | 21 | 93 |
查看答案和解析>>
科目:初中数学 来源: 题型:
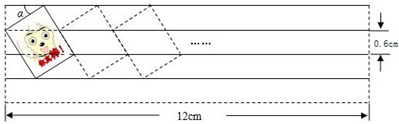
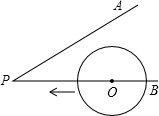 如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为
如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com