
【题目】如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.求证:BE=BD

科目:初中数学 来源: 题型:
【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图:
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H .
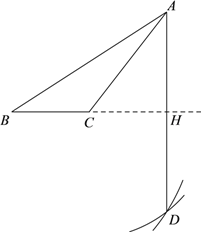
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是___________.他的依据是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=![]() 时, 若CD=
时, 若CD=![]() ,求AD长.
,求AD长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() (b为常数)的图象与x轴交于点A(2,0),与y轴交于点B,与反比例函数
(b为常数)的图象与x轴交于点A(2,0),与y轴交于点B,与反比例函数![]() 的图象交于点C(-2,m).
的图象交于点C(-2,m).
(1)求点C的坐标及反比例函数的表达式;
(2)过点C的直线与y轴交于点D,且![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
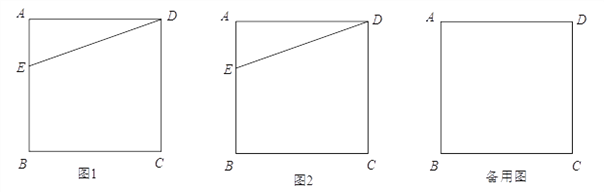
【题目】如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG.
(1)依题意在图1中补全图形;
(2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明;
(3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在“五一”小长假期间,每天接待的旅客人数统计如下表.
日期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 |
人数(万人) | 1.2 | 2 | 2.5 | 2 | 1.1 |
表中表示人数的一组数据中,众数和中位数分别为( )
A.2.5万,2万B.2.5万,2.5万C.2万,2.5万D.2万,2万
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com