
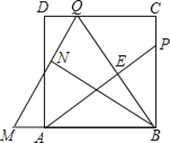
【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。
【答案】(1)证明见解析;(2)MQ=![]() ;(3)AM=
;(3)AM=![]() .
.
【解析】试题分析:(1)证明△ABP≌△BCQ,则∠BAP=∠CBQ,从而证明∠CBQ+∠APB=90°,进而得证;
(2)设MQ=MB=x,则MN=x﹣2.在直角△MBN中,利用勾股定理即可列方程求解;
(3)设AM=y,BN=BC=m+n,在直角△BNM中,MB=y+m+n,MN=MQ﹣QN=(y+m+n)﹣m=y+n,利用勾股定理即可求解.
试题解析:(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠C=90°,AB=BC,在△ABP和△BCQ中,∵AB=BC,∠ABC=∠C,BP=CQ,∴△ABP≌△BCQ,∴∠BAP=∠CBQ.
∵∠BAP+∠APB=90°,∴∠CBQ+∠APB=90°,∴∠BEP=90°,∴AP⊥BQ;
(2)解:∵正方形ABCD中,AB=3,BP=2CP,∴BP=2,由(1)可得NQ=CQ=BP=2,NB=3.
又∵∠NQB=∠CQB=∠ABQ,∴MQ=MB.
设MQ=MB=x,则MN=x﹣2.
在直角△MBN中, ![]() ,即
,即![]() ,解得:x=
,解得:x=![]() ,即MQ=
,即MQ=![]() ;
;
(3)∵BP=m,CP=n,由(1)(2)得MQ=BM,CQ=QN=BP=m,设AM=y,BN=BC=m+n,在直角△BNM中,MB=y+m+n,MN=MQ﹣QN=(y+m+n)﹣m=y+n, ![]() ,即
,即![]() ,则y=
,则y=![]() ,AM=
,AM=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列各组中的四条线段成比例的是( )
A.a=1,b=3,c=2,d=4B.a=4,b=6,c=5,d=10
C.a=2,b=4,c=3,d=6D.a=2,b=3,c=4,d=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:![]() >0.
>0.
解:设![]() =0,解得:
=0,解得:![]() =0,
=0,![]() =5,则抛物线y=
=5,则抛物线y=![]() 与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=
与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=![]() 的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即
的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即![]() >0,所以,一元二次不等式
>0,所以,一元二次不等式![]() >0的解集为:x<0或x>5.
>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式![]() <0的解集为 .
<0的解集为 .
(3)用类似的方法解一元二次不等式:![]() >0.
>0.
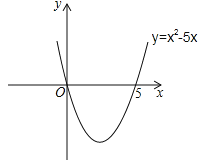
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )
A. (2,﹣3) B. (﹣2,3) C. (﹣2,﹣3) D. (2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温家宝总理在十届全国人大四次会议上谈到解决关于“三农”问题时说,2006年中央财政用于“三农”的支出将达到33 970 000万元,这个数据用科学记数法可表示为万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com