Question

【题目】如图，已知∠1＝∠2，要使△ABD≌△ACD，需从下列条件中增加一个，错误的选法是（ ）

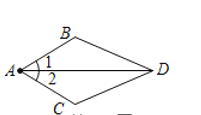
A.∠ADB＝∠ADCB.∠B＝∠CC.AB＝ACD.DB＝DC

Answer 1

【答案】D

【解析】

由全等三角形的判定方法ASA证出△ABD≌△ACD，得出A正确；由全等三角形的判定方法AAS证出△ABD≌△ACD，得出B正确；由全等三角形的判定方法SAS证出△ABD≌△ACD，得出C正确．由全等三角形的判定方法得出D不正确；

A正确；理由：

在△ABD和△ACD中，

∵∠1=∠2，AD=AD，∠ADB=∠ADC，

∴△ABD≌△ACD（ASA）；

B正确；理由：

在△ABD和△ACD中，

∵∠1=∠2，∠B=∠C，AD=AD

∴△ABD≌△ACD（AAS）；

C正确；理由：

在△ABD和△ACD中，

∵AB=AC，∠1=∠2，AD=AD，

∴△ABD≌△ACD（SAS）；

D不正确，由这些条件不能判定三角形全等；

故选：D．