练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知一次函数的图象经过A（﹣1，4），B（1，﹣2）两点．

    （1）求该一次函数的解析式；

    （2）直接写出函数图象与两坐标轴的交点坐标．

    【答案】（1）一次函数解析式为y＝﹣3x+1；（2）一次函数与x轴的交点坐标为（，0），与y轴的交点坐标为（0，1）．

    【解析】

    （1）利用待定系数法容易求得一次函数的解析式；

    （2）分别令x=0和y=0，可求得与两坐标轴的交点坐标．

    （1）设直线的解析式为y=kx+b．

    ∵图象经过点（﹣1，4），（1，﹣2）两点，∴把两点坐标代入函数解析式可得：，解得：，∴一次函数解析式为y=﹣3x+1；

    （2）在y=﹣3x+1中，令y=0，可得：﹣3x+1=0，解得：x；

    令x=0，可得：y=1，∴一次函数与x轴的交点坐标为（，0），与y轴的交点坐标为（0，1）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1＝∠2，要使△ABD≌△ACD，需从下列条件中增加一个，错误的选法是（ ）

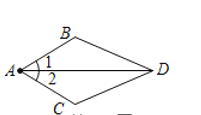
    A.∠ADB＝∠ADCB.∠B＝∠CC.AB＝ACD.DB＝DC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰直角中，，，点是 内一点，连接， 且，连接、交于点.

    （1）如图 1，求的度数；

    （2）如图 2，连接交于点，连接，若平分，求证：；

    （3）如图 3，在（2）的条件下，交、分别于点、，，连接，若的面积与的面积差为 6，，求四边形的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个点到圆的最小距离为，最大距离为，则该圆的半径是____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个安装有进出水管的30升容器，水管单位时间内进出的水量是一定的，设从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到水量y（升）与时间x（分）之间的函数关系如图所示．根据图象信思给出下列说法，其中错误的是（　　）

    A. 每分钟进水5升

    B. 每分钟放水1.25升

    C. 若12分钟后只放水，不进水，还要8分钟可以把水放完

    D. 若从一开始进出水管同时打开需要24分钟可以将容器灌满

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC在平面直角坐标系中的位置如图所示．

    （1）在图中画出△ABC与关于y轴对称的图形△A1B1C1，并写出顶点A1、B1、C1的坐标；

    （2）若将线段A1C1平移后得到线段A2C2，且A2（a，2），C2（-2，b），求a+b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D在AB上，点E在BC上，BD＝BE．

    （1）请你再添加一个条件，使得△BEA≌△BDC，并给出证明．你添加的条件是　 　．

    （2）根据你添加的条件，再写出图中的一对全等三角形　 　．（只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD∥BC，∠EAD＝∠C．

    （1）试判断AE与CD的位置关系，并说明理由；

    （2）若∠FEC＝∠BAE，∠EFC＝50°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知A(3，0),B(0，-1)，连接AB,过B点作AB的垂线段,使BA=BC,连接AC.

    (1)如图1，求C点坐标；

    (2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.

    (3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

    查看答案和解析>>

    同步练习册答案