
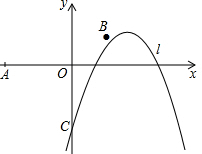
 如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.
如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.分析 (1)把点B的坐标代入函数解析式,列出关于h的方程,借助于方程可以求得h的值;利用抛物线函数解析式得到该图象的对称轴和顶点坐标;
(2)把点C的坐标代入函数解析式得到:yC=-h2+1,则由二次函数的最值的求法易得yc的最大值,并可以求得此时抛物线的解析式,根据抛物线的增减性来求y1与y2的大小;
(3)根据已知条件“O(0,0),A(-5,0),线段OA被l只分为两部分,且这两部分的比是1:4”可以推知把线段OA被l只分为两部分的点的坐标分别是(-1,0),(-4,0).由二次函数图象上点的坐标特征可以求得h的值.
解答 解:(1)把点B的坐标B(2,1)代入y=-(x-h)2+1,得
1=-(2-h)2+1.
解得h=2.
则该函数解析式为y=-(x-2)2+1(或y=-x2+4x-3).
故抛物线l的对称轴为x=2,顶点坐标是(2,1);
(2)点C的横坐标为0,则yC=-h2+1.
当h=0时,yC=有最大值1,
此时,抛物线l为:y=-x2+1,对称轴为y轴,开口方向向下,
所以,当x≥0时,y随x的增大而减小,
所以,x1>x2≥0,y1<y2;
(3)∵线段OA被l只分为两部分,且这两部分的比是1:4,且O(0,0),A(-5,0),
∴把线段OA被l只分为两部分的点的坐标分别是(-1,0),(-4,0).
把x=-1,y=0代入y=-(x-h)2+1,得
0=-(-1-h)2+1,
解得h1=0,h2=-2.
但是当h=-2时,线段OA被抛物线l分为三部分,不合题意,舍去.
同样,把x=-4,y=0代入y=-(x-h)2+1,得
h=-5或h=-3(舍去).
综上所述,h的值是0或-5.
点评 本题考查了二次函数综合题.该题涉及到了待定系数法求二次函数解析式,二次函数图象上点的坐标特征,二次函数最值的求法以及点的坐标与图形的性质等知识点,综合性比较强,难度较大.解答(3)题时,注意对h的值根据实际意义进行取舍.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
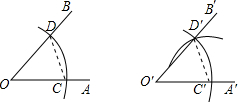 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )| A. | 边边边 | B. | 边角边 | C. | 角边角 | D. | 角角边 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )| A. |  | B. | 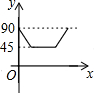 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
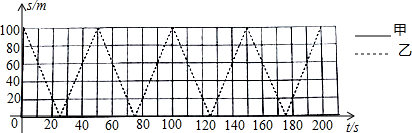
| 两人相遇次数 (单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和 (单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=16cm.
如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=16cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
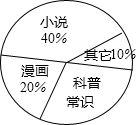 为了解学生课外阅读的喜好,某校从八年级1200名学生中随机抽取50名学生进行问卷调查,整理数据后绘制如图所示的统计图.由此可估计该年级喜爱“科普常识”的学生约有360人.
为了解学生课外阅读的喜好,某校从八年级1200名学生中随机抽取50名学生进行问卷调查,整理数据后绘制如图所示的统计图.由此可估计该年级喜爱“科普常识”的学生约有360人.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
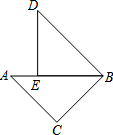 如图,△ABC和△DBE都是等腰直角三角形,点E在AB上,若△ABC经旋转后能与△DBE重合,则旋转中心为( )
如图,△ABC和△DBE都是等腰直角三角形,点E在AB上,若△ABC经旋转后能与△DBE重合,则旋转中心为( )| A. | 点A | B. | 点B | C. | 点C | D. | 点E |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com