练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

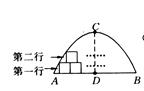
    如图2 - 62所示，某地下储藏室横截面呈抛物线形．已知跨度AB=6米，最高点C到地面的距离CD＝3米．   

        (1)建立适当的平面直角坐标系，求抛物线的解析式；

    (2)在储藏室内按如图2 - 62所示的方式摆放棱长为l米的长方体货物箱，则第二行最多能摆放多少个货物箱?


    解：(1)以AB所在的直线为x轴，点D为原点，建立平面直角坐标系，如图2 - 65所示．设抛物线的解析式为y＝ax2+c．将A(—3，0)，C(0，3)代入解析式，得 故所求抛物线的解析式为．  (2)当y=2时，+3＝2，解得x＝± ．因为［—(—)]÷l＝2，而3<2<4，所以第二行最多能摆放3个货物箱．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列调查中，①调查本班同学的视力；②调查一批节能灯管的使用寿命；③为保证“神舟9号”的成功发射，对其零部件进行检查；④对乘坐某班次客车的乘客进行安检.其中适合采用抽样调查的是(    )

      A.①             B.②              C.③               D.④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在二次函数①y＝3x2；②中，图象在同一水平线上的开口大小顺序用题号表示应该为(    )

    A．①＞②＞③                     B．①＞③＞②

    C．②＞③＞①                     D．②＞①＞③

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图2 - 60所示的是二次函数y＝ax2+bx+c图象的一部分，图象过点A(—3，0)，对称轴为x=—1．给出四个结论：①b2＞4ac；②2a+b＝0；③a-b+c＝0；④5a<b．其中正确的结论是    (    )

            A.②④         B．①④        C.②③         D．①③

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某物体从上午7时至下午4时的温度M (℃)是时间t(h)的函数M＝t2－5t+100(其中t＝0表示中午12时，t＝1表示下午1时)，则上午10时此物体的温度是      ℃．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    抛物线y＝x2－4x＋3的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为(　　)

    A．(4，－1)  B．(0，－3)  C．(－2，－3)  D．(－2，－1)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3－4－7，已知二次函数y＝x2＋bx＋c的图象经过点(－1,0)，(1，－2)，当y随x的增大而增大时，x的取值范围是____________．

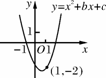
    图3－4－7

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用配方法把二次函数y＝l+2x－x2化为y＝a(x－h)2+k的形式，作出它的草图，回答下列问题．

        (1)求抛物线的顶点坐标和它与x轴的交点坐标；

        (2)当x取何值时，y随x的增大而增大?

    (3)当x取何值时，y的值大于0?

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    函数的图象如图 l－2－32所示，则下列结论错误的是（  ）

       A．a＞0             B．b2－4ac＞0

       C、的两根之和为负

       D、的两根之积为正

    查看答案和解析>>

    同步练习册答案