
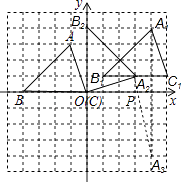
����Ŀ����ͼ��ƽ��ֱ������ϵ�ڣ�С����������ı߳�Ϊ1����λ���ȣ���ABC���������������ֱ�ΪA����1��3����B����4��0����C��0��0��
��1����������ABC����ƽ��1����λ���ȣ�������ƽ��5����λ���Ⱥ�õ��ġ�A1B1C1��
��2����������ABC��ԭ��O˳ʱ�뷽����ת90��õ���A2B2O��
��3����x���ϴ���һ��P�������P��A1���A2����֮����С����ֱ��д��P������꣮
���𰸡�
��1���⣺��ͼ��ʾ����A1B1C1Ϊ�������������Σ�
��2���⣺��ͼ��ʾ����A2B2OΪ�������������Σ�

��3���⣺��A2����Ϊ��3��1����A3����Ϊ��4����4����
��A2A3����ֱ�ߵĽ���ʽΪ��y=��5x+16��
��y=0����x= ![]() ��
��
��P������꣨ ![]() ��0����
��0����
�����������⿼����������ת��ƽ�Ʊ任��ͼ��������������ṹȷ�ҳ���Ӧ���λ���ǽ���Ĺؼ�����1���ֱ�A��B��C����ƽ��1����λ��������ƽ��5����λ��Ȼ��˳�����ӣ���2����������ṹ�ҳ���A��B��C�Ե�OΪ��ת����˳ʱ����ת90���Ķ�Ӧ�㣬Ȼ��˳�����Ӽ��ɣ���3���������·����������������A1�����x��ĶԳƵ�A3 �� ������A2A3��x��Ľ��㼴Ϊ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������x���һ������A��1��0�����Գ�����x=-1�������������x�����һ���������ǣ�������
A.��-3��0��
B.��-2��0��
C.x=-3
D.x=-2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Dz�ݮ�����ļ��ڣ�ijˮ�������̵�������δ������г���������ݮ40�䣬��֪��һ�����ν����۷ֱ�Ϊÿ��50Ԫ��40Ԫ���ҵڶ��αȵ�һ�ζึ��700Ԫ��
��1�����һ�����ι�����ݮ�������ֱ�Ϊa�䡢b�䣬��a��b��ֵ��
��2�����̵����40���ݮ�Ȱ�ÿ��60Ԫ������x�䣬����İ�ÿ��35Ԫȫ�����꣮
�����̵�������ȫ����ݮ��������y��Ԫ����x���䣩֮��ĺ�����ϵʽ��
�ڵ�x��ֵ����Ϊ����ʱ���̵�Ų����������ע����������ۣ��������������룭�����ܳɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��֪a��b����![]() �������x�ķ���(a��2)x��b2��a��1��
�������x�ķ���(a��2)x��b2��a��1��
(2)ʵ��a��b��Ϊ�෴����c��d��Ϊ������x�ľ���ֵΪ![]() �������ʽx2��(a��b)cdx��
�������ʽx2��(a��b)cdx��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��P��6��3��������P��PM��x���ڵ�M��PN��y���ڵ�N������������y= ![]() ��ͼ��PM�ڵ�A����PN�ڵ�B�����ı���OAPB�����Ϊ12����k= ��
��ͼ��PM�ڵ�A����PN�ڵ�B�����ı���OAPB�����Ϊ12����k= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��x=2��������y=x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C���ҵ�A������Ϊ����1��0��
ע�����κ���y=ax2+bx+c��a��0���Ķ�������Ϊ���� ![]() ��
�� ![]() ��
��
��1���������ߵĽ���ʽ��
��2��ֱ��д��B��C��������ꣻ
��3�����O��B��C�����Բ�������������ú��еĴ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿѧ�����ʣ���ѧУ�ձ鿪չ�������������ijУΪ�˽�ȫУ1000��ѧ��ÿ�ܿ��������ʱ��������������������е�50��ѧ��������50��ѧ��ÿ�ܿ��������ʱ��x����λ��Сʱ��������ͳ�ƣ������������ݻ�����һ����������ͳ��ͼ����֪��ÿ�ܿ��������ʱ����6��x��8Сʱ��ѧ������ռ24%������������Ϣ��ͳ��ͼ����������⣺
��1�����ε����������飬������������
��2���벹ȫƵ���ֲ�ֱ��ͼ�п�ȱ�IJ��֣�
��3������50��ѧ��ÿ�ܿ��������ʱ���ƽ������
��4������ȫУѧ��ÿ�ܿ��������ʱ�䲻����6Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���BAD=120�㣬��E��F�ֱ��ڱ�AB��BC�ϣ���BEF���GEF����ֱ��EF�Գƣ���B�ĶԳƵ��ǵ�G���ҵ�G�ڱ�AD�ϣ���EG��AC��AB=6 ![]() ����FG�ij�Ϊ ��
����FG�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com