
【题目】如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,∠BOC= .

 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】计算下列各式.
(1)3 ![]() +(﹣
+(﹣ ![]() )﹣(﹣
)﹣(﹣ ![]() )+2
)+2 ![]()
(2)﹣82+3×(﹣2)2+(﹣6)÷(﹣ ![]() )2
)2
(3)4 ![]() ×[﹣9×(﹣
×[﹣9×(﹣ ![]() )2﹣0.8]÷(﹣5
)2﹣0.8]÷(﹣5 ![]() );
);
(4)( ![]() +
+ ![]() ﹣
﹣ ![]() )×(﹣12)
)×(﹣12)
(5)﹣24﹣[(﹣3)2﹣(1﹣23× ![]() )÷(﹣2)]
)÷(﹣2)]
(6)(﹣96)×(﹣0.125)+96× ![]() +(﹣96)×
+(﹣96)× ![]()
(7)(3a﹣2)﹣3(a﹣5)
(8)(4a2b﹣5ab2)﹣(3a2b﹣4ab2)
(9)x﹣2[y+2x﹣(3x﹣y)]
(10)![]() m﹣2(m﹣
m﹣2(m﹣ ![]() n2)﹣(
n2)﹣( ![]() m﹣
m﹣ ![]() n2).
n2).![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是等边三角形ABC所在平面上一点,若P和△ABC的三个顶点所组成的△PAB、△PBC、△PAC都是等腰三角形,则这样的点P的个数为( )
A.1 B.4 C.7 D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进经济社会平衡发展,保障低收入群体生活水平不受疫情影响,郑州市人民政府计划向社会发放近4亿消费券,如今第一期消费券已于4月3日上午10点准时发放,总额5000万元,请将5000万用科学记数法表示为( )
A.5×103B.5×107C.5×104D.5×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.

查看答案和解析>>
科目:初中数学 来源: 题型:
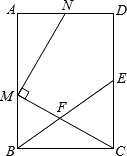
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() =2,求
=2,求![]() 的值;
的值;
(3)若![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA= , PC=;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com