
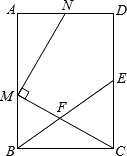
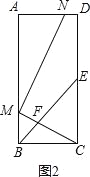
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() =2,求
=2,求![]() 的值;
的值;
(3)若![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
【答案】(1)详见解析;(2)3;(3)n=4.
【解析】
试题分析:(1)如图1,易证△BMF≌△ECF,则有BM=EC,然后根据E为CD的中点及AB=DC就可得到AM=EC;(2)如图2,设MB=a,易证△ECF∽△BMF,根据相似三角形的性质可得EC=2a,由此可得AB=4a,AM=3a,BC=AD=2a.易证△AMN∽△BCM,根据相似三角形的性质即可得到AN=![]() a,从而可得ND=AD﹣AN=
a,从而可得ND=AD﹣AN=![]() a,就可求出
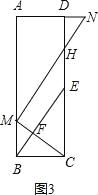
a,就可求出![]() 的值;(3)如图3,设MB=a,同(2)可得BC=2a,CE=na.由MN∥BE,MN⊥MC可得∠EFC=∠HMC=90°,从而可证到△MBC∽△BCE,然后根据相似三角形的性质即可求出n的值.
的值;(3)如图3,设MB=a,同(2)可得BC=2a,CE=na.由MN∥BE,MN⊥MC可得∠EFC=∠HMC=90°,从而可证到△MBC∽△BCE,然后根据相似三角形的性质即可求出n的值.
试题解析:(1)当F为BE中点时,如图1,
则有BF=EF.
∵四边形ABCD是矩形,
∴AB=DC,AB∥DC,
∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,
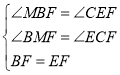 ,
,
∴△BMF≌△ECF,
∴BM=EC.
∵E为CD的中点,
∴EC=![]() DC,
DC,
∴BM=EC=![]() DC=
DC=![]() AB,
AB,
∴AM=BM=EC;
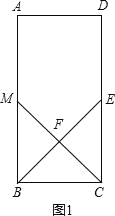
(2)如图2,
设MB=a,
∵四边形ABCD是矩形,
∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,
∴△ECF∽△BMF,
∴![]() =2,
=2,
∴EC=2a,
∴AB=CD=2CE=4a,AM=AB﹣MB=3a.
∵![]() =2,
=2,
∴BC=AD=2a.
∵MN⊥MC,
∴∠CMN=90°,
∴∠AMN+∠BMC=90°.
∵∠A=90°,
∴∠ANM+∠AMN=90°,
∴∠BMC=∠ANM,
∴△AMN∽△BCM,
∴![]() ,
,
∴![]() ,
,
∴AN=![]() a,ND=AD﹣AN=2a﹣
a,ND=AD﹣AN=2a﹣![]() a=
a=![]() a,
a,
∴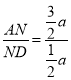 =3;
=3;
(3)当![]() =n时,如图3,
=n时,如图3,
设MB=a,同(2)可得BC=2a,CE=na.
∵MN∥BE,MN⊥MC,
∴∠EFC=∠HMC=90°,
∴∠FCB+∠FBC=90°.
∵∠MBC=90°,
∴∠BMC+∠FCB=90°,
∴∠BMC=∠FBC.
∵∠MBC=∠BCE=90°,
∴△MBC∽△BCE,
∴![]() ,
,
∴![]() ,
,
∴n=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.根据统计图解答下列问题:
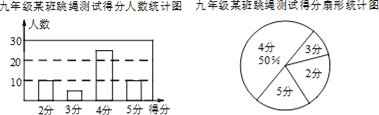
(1)在扇形统计图中,得5分学生的测试成绩所占扇形的圆心角度数为 ;
(2)被测学生跳绳测试成绩的众数是 分;中位数是 分;
(3)本次测试成绩的平均分是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表
抛掷次数 | 100 | 200 | 300 | 400 | 500 |
正面朝上的频数 | 53 | 98 | 156 | 202 | 249 |
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.200B.300C.400D.500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,“新型冠状肺炎”流行,这种病毒的直径大约为150纳米,1纳米=0.000000001米=10-9米,把150纳米用科学记数法表示正确的是( )
A.1.5×10-2米B.1.5×10-7米C.1.5×10-9米D.1.5×10-11米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,当平行四边形CBPQ的面积为30时,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com