
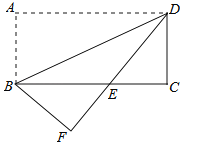
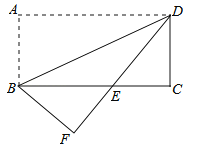
【题目】(2016四川省乐山市第20题)如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)由AD∥BC,知∠ADB=∠DBC,根据折叠的性质∠ADB=∠BDF,所以∠DBC=∠BDF,得BE=DE,即可用AAS证△DCE≌△BFE;
(2)在Rt△BCD中,CD=2,∠ADB=∠DBC=30°,知BC=![]() ,在Rt△BCD中,CD=2,∠EDC=30°,知CE=
,在Rt△BCD中,CD=2,∠EDC=30°,知CE=![]() ,所以BE=BC﹣EC=
,所以BE=BC﹣EC=![]() .
.
试题解析:(1)∵AD∥BC,∴∠ADB=∠DBC,根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,∴∠DBC=∠BDF,∴BE=DE,在△DCE和△BFE中,∵∠BEF=∠DEC,∠F=∠C,BE=DE,∴△DCE≌△BFE;
(2)在Rt△BCD中,∵CD=2,∠ADB=∠DBC=30°,∴BC=![]() ,在Rt△BCD中,∵CD=2,∠EDC=30°,∴DE=2EC,∴
,在Rt△BCD中,∵CD=2,∠EDC=30°,∴DE=2EC,∴![]() ,∴CE=
,∴CE=![]() ,∴BE=BC﹣EC=
,∴BE=BC﹣EC=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
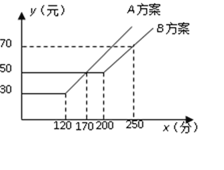
【题目】如图,某电信公司提供了![]() 两种方案的移动通讯费用
两种方案的移动通讯费用![]() (元)与通话时间
(元)与通话时间![]() (元)之间的关系,则以下说法错误的是( )
(元)之间的关系,则以下说法错误的是( )
A. 若通话时间少于120分,则![]() 方案比
方案比![]() 方案便宜20元
方案便宜20元
B. 若通话时间超过200分,则![]() 方案比
方案比![]() 方案便宜12元
方案便宜12元
C. 若通讯费用为60元,则![]() 方案比
方案比![]() 方案的通话时间多
方案的通话时间多
D. 若两种方案通讯费用相差10元,则通话时间是145分或185分
查看答案和解析>>
科目:初中数学 来源: 题型:
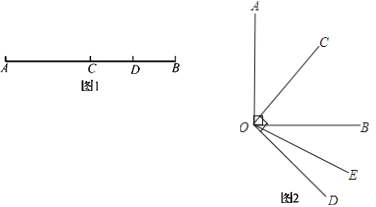
【题目】(1)如图1,已知点D是线段AC的中点,点B在线段DC上,且AB=4BC,若BD=6 cm,求AB的长;
(2)如图2,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,试求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
①矩形的对角线互相平分且相等;
②对角线相等的四边形是矩形;
③菱形的每一条对角线平分一组对角;
④一条对角线平分一组对角的平行四边形是菱形.
其中正确的命题为________(注:把你认为正确的命题序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各题的结果正确的是( )
A. 3x+3y=6xy B. 16y2-7y2=9 C. -2(m-n)=-2m-2n D. 19a2b-9a2b=10a2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若把Rt△ABC三边的长度都扩大为原来的5倍,则锐角∠A的正切值( )
A. 扩大为原来的5倍 B. 不变 C. 缩小为原来的5倍 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120)。已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1) 当速度为50km/h、100km/h时,该汽车的耗油量分别为_____L/km、____L/km.
(2) 求线段AB所表示的y与x之间的函数表达式
(3) 速度是多少时,该汽车的耗油量最低?最低是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com