
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 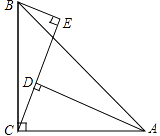
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF= . 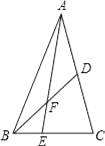
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点. 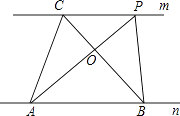
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探索:
(1)已知一个正分数![]() (m>n>0),如果分子、分母同时增加1,分数的值是增大还是减小?请证明你的结论.
(m>n>0),如果分子、分母同时增加1,分数的值是增大还是减小?请证明你的结论.
(2)若正分数![]() (m>n>0)中分子和分母同时增加2,3…k(整数k>0),情况如何?
(m>n>0)中分子和分母同时增加2,3…k(整数k>0),情况如何?
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,问同时增加相等的窗户面积和地板面积,住宅的采光条件是变好还是变坏?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明一家自驾游去了离家170千米的某地,他们离家的距离y(千米)与汽车行驶时间x(小时)之间的关系为y=40x+60,当他们离目的地还有20千米时,汽车一共行驶的时间是_____小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面一列分式:![]() , ﹣
, ﹣![]() ,
, ![]() , ﹣
, ﹣![]() , …(其中x≠0).
, …(其中x≠0).
(1)根据上述分式的规律写出第6个分式;
(2)根据你发现的规律,试写出第n(n为正整数)个分式,并简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了解员工对“六五”普法知识的知晓情况,从本公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
(1) 表中a=__________,b=__________,c=__________
(2) 请补全频数分布直方图
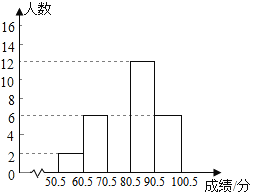
(3)该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数
组别 | 分数段/分 | 频数/人数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com