
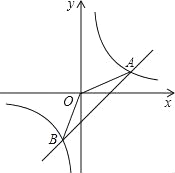
【题目】如图,平面直角坐标系中,已知A(4,a),B(﹣2,﹣4)是一次函数y=k1x+b的图象和反比例函数y=﹣![]() 的图象的交点.
的图象的交点.
(1)求反比例函数和直线AB的解折式;
(2)将直线OA沿y轴向下平移m个单位后,得到直线l,设直线l与直线AB的交点为P,若S△OAP=2S△OAB,求m的值.
【答案】(1)y2=![]() ;y1=x﹣2;(2)6.
;y1=x﹣2;(2)6.
【解析】
(1)把A(4,a),B(-2,-4)分别代入一次函数y=k1x+b和反比例函数y=-![]() ,运用待定系数法分别求其解析式;
,运用待定系数法分别求其解析式;
(2)利用待定系数法求出直线OA的解析式,根据平移的性质得出直线l的解析式.根据S△OAP=2S△OAB,得出B为AP的中点,求出P(-8,-10).将P点坐标代入y=![]() x-m,即可求出m的值.
x-m,即可求出m的值.
解:(1)将B(﹣2,﹣4)代入y=﹣![]() ,
,
可得﹣![]() =﹣4,
=﹣4,
解得k2=﹣8,
∴反比例函数的解折式为y2=![]() ,
,
②当x=4时,y=![]() =2,
=2,
∴A(4,2),
将A(4,2)、B(﹣2,﹣4)代入y1=kx+b,
可得:![]() ,解得
,解得![]() ,
,
∴直线AB的解折式为y1=x﹣2;
(2)∵A(4,2),
∴直线OA的解析式为y=![]() x,
x,
∵将直线OA沿y轴向下平移m个单位后,得到直线l,
∴直线l的解析式为y=![]() x﹣m.
x﹣m.
∵S△OAP=2S△OAB,
∴B为AP的中点,
∵A(4,2),B(﹣2,﹣4),
∴P(﹣8,﹣10).
将P(﹣8,﹣10)代入y=![]() x﹣m,
x﹣m,
得﹣10=![]() ×(﹣8)﹣m,解得m=6.
×(﹣8)﹣m,解得m=6.
故所求m的值为6.


科目:初中数学 来源: 题型:
【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
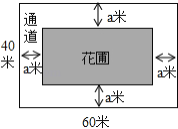
(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=![]() (x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
(x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:

①逐渐变小;
②由大变小再由小变大;
③由小变大再由大变小;
④不变.
你认为正确的是_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.

(1)求证:四边形ADCF是平行四边形;
(2)当AB与AC有何数量关系时,四边形ADCF为矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.

(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
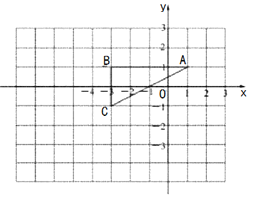
【题目】如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1)、B(-3,1)、C(-3.-1).
(1)若△ABC的外接圆的圆心为P,则点P的坐标为_________.
(2)如图所示,在11×8的网格图内,以坐标原点O点为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为![]() 得到
得到![]() 在图中画出
在图中画出![]() 若将
若将![]() 沿
沿![]() 轴方向平移,需平移_______单位长度,能使得
轴方向平移,需平移_______单位长度,能使得![]() 所在的直线与⊙P相切.
所在的直线与⊙P相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P为拋物线![]() 为常数,
为常数,![]() )上任意一点,将抛物线绕顶点G逆时针旋转90°后得到的图象与
)上任意一点,将抛物线绕顶点G逆时针旋转90°后得到的图象与![]() 轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
(1)抛物线![]() 的对称轴是直线________,当m=2时,点P的横坐标为4时,点Q的坐标为_________;
的对称轴是直线________,当m=2时,点P的横坐标为4时,点Q的坐标为_________;
(2)设点Q![]() 请你用含m,
请你用含m,![]() 的代数式表示
的代数式表示![]() 则
则![]() ________;
________;
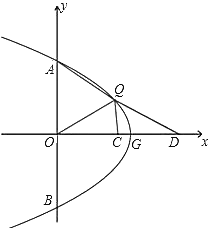
(3)如图,点Q在第一象限,点D在![]() 轴的正半轴上,点C为OD的中点,QO平分∠AQC,当AQ=2QC,QD=
轴的正半轴上,点C为OD的中点,QO平分∠AQC,当AQ=2QC,QD=![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于![]() , 问至少取出了多少个黑球?
, 问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
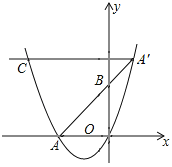
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com