
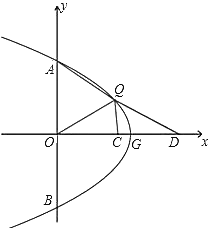
����Ŀ����PΪ������![]() Ϊ������
Ϊ������![]() ��������һ�㣬���������ƶ���G��ʱ����ת90���õ���ͼ����
��������һ�㣬���������ƶ���G��ʱ����ת90���õ���ͼ����![]() �ύ��A��B���㣨��A�ڵ�B���Ϸ�������QΪ��P��ת��Ķ�Ӧ�㣮
�ύ��A��B���㣨��A�ڵ�B���Ϸ�������QΪ��P��ת��Ķ�Ӧ�㣮
��1��������![]() �ĶԳ�����ֱ��________����m=2ʱ����P�ĺ�����Ϊ4ʱ����Q������Ϊ_________��
�ĶԳ�����ֱ��________����m=2ʱ����P�ĺ�����Ϊ4ʱ����Q������Ϊ_________��
��2�����Q![]() �����ú�m��
�����ú�m��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��![]() ________��
________��
��3����ͼ����Q�ڵ�һ���ޣ���D��![]() ����������ϣ���CΪOD���е㣬QOƽ�֡�AQC����AQ=2QC��QD=
����������ϣ���CΪOD���е㣬QOƽ�֡�AQC����AQ=2QC��QD=![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
���𰸡���1��x=m��Q��-2,2������2��a=m-![]() ����3��m=1.
����3��m=1.
��������
��1���䷽���ɵó������ߵĶԳ���������m��ֵȷ����ԭ�����ߵĽ���ʽ�����������P��G����������P��PE��x����E����Q��QF��x����F��������ת������֪����GQF�ա�PGE����QF��GE��PE��GF���ɾݴ���õ�Q��������
��2����֪Q�����������ɵõ�QF��FG�ij������գ�1���ķ����������P��������Ȼ�����ԭ�����ߵĽ���ʽ���������a��b��m�Ĺ�ϵʽ��
��3���ӳ�QC��E��ʹ��QC��CE����ôAQ��QE����֤��QCD�ա�ECO����ôQD��OE��m����AQ��QE����QOƽ�֡�AQC����֤�á�AQO�ա�EQO����OA��OE��m����A������Ϊ��0��m����Ȼ��A��������루2���Ĺ�ϵʽ�����������m��ֵ��
��1��![]() =
=![]() ���Գ���Ϊֱ��x=m��
���Գ���Ϊֱ��x=m��
��m��2ʱ��y����x��2��2����G��2��0����
�ߵ�P�ĺ�����Ϊ4����P�������������ཫx��4���������߽���ʽ����y����4��2��2��4����P��4��4������ͼ������QG��PG������Q��QF��x����F������P��PE��x����E�����������ɵ�����GQF�ա�PGE����FQ��EG��2��FG��EP��4����FO��2����Q����2��2����
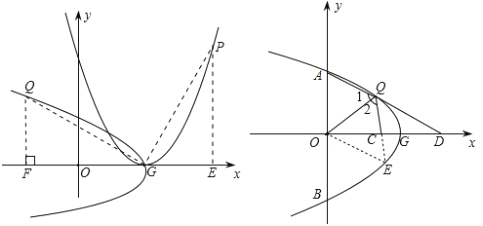
��2����֪Q��a��b������GE��QF��b��FG��m��a��
�ɣ�1��֪��PE��FG��m��a��GE��QF��b����P��m+b��m��a��������ԭ�����ߵĽ���ʽ��������m��a����m+b��2��2m��m+b��+m2��m��a��m2+b2+2mb��2m2��2mb+m2��a��m��b2�����ú�m��b�Ĵ���ʽ��ʾa��a��m��b2��
��3����ͼ���ӳ�QC����E��ʹCE��CQ������OE��
��CΪOD�е�����OC��CD��
�ߡ�ECO����QCD�����ECO�ա�QCD����OE��DQ��m��
��AQ��2QC����AQ��QE��
��QOƽ�֡�AQC�����1����2�����AQO�ա�EQO����AO��EO��m����A��0��m����
��A��0��m������ͼ��������0��m��m2����m1��1��m2��0���ᣩ����m��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x2+bx+c��x�ύ��A��1��0����B��m��0������y�ύ��C��
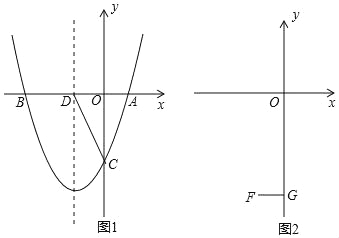
��1����m=��3���������ߵĽ���ʽ����д�������ߵĶԳ��
��2����ͼ1���ڣ�1���������£��������ߵĶԳ��ύx����D���ڶԳ�����������������һ��E��ʹS��ACE=![]() S��ACD�����E�����ꣻ
S��ACD�����E�����ꣻ
��3����ͼ2����F����1����4����FG��y��G�����߶�OG���Ƿ���ڵ�P��ʹ��OBP=��FPG�������ڣ���m��ȡֵ��Χ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
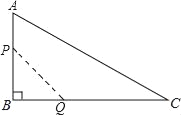
����Ŀ����ͼ���ڡ�ABC�У���B��90�㣬AB��12mm��BC��24mm������P�ӵ�A��ʼ�ر�AB��B��2mm/s���ٶ��ƶ��������B�غϣ�������Q�ӵ�B��ʼ�ر�BC��C��4mm/s���ٶ��ƶ��������C�غϣ������P��Q�ֱ��A��Bͬʱ���������˶���ʱ��Ϊxs���ı���APQC�����Ϊymm2��
��1��y��x֮��ĺ�����ϵʽ��
��2�����Ա���x��ȡֵ��Χ��
��3���ı���APQC������ܷ����172mm2�����ܣ�����˶���ʱ�䣻�����ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪A��4��a����B����2����4����һ�κ���y��k1x+b��ͼ��ͷ���������y����![]() ��ͼ��Ľ��㣮
��ͼ��Ľ��㣮
��1������������ֱ��AB�Ľ���ʽ��
��2����ֱ��OA��y������ƽ��m����λ�õ�ֱ��l����ֱ��l��ֱ��AB�Ľ���ΪP����S��OAP��2S��OAB����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
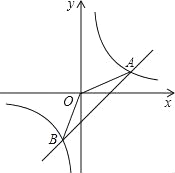
����Ŀ����֪����ͼ��OΪ�����ζԽ��ߵĽ��㣬BEƽ����DBC����DC�ڵ�E���ӳ�BC����F��ʹCF=CE������DF����BE���ӳ����ڵ�G������OG��
��1����֤����BCE�ա�DCF��
��2���ж�OG��BF��ʲô��ϵ��֤����Ľ�����
��3����DF2=8-4![]() ����������ABCD�������
����������ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
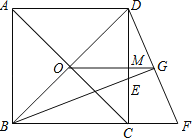
����Ŀ����ͼ�����ı���ABCD�У�AB=AD��CB=CD��E��CD��һ�㣬BE��AC��F������DF��
��1��֤������BAC=��DAC��
��2������BEC=��ABE����֤���ı���ABCD�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С������Ϸ����ͼ��������ͬ�Ŀ�Ƭ��ÿ�����ţ���һ�鿨Ƭ����ֱ��������1��3��5���ڶ��鿨Ƭ����ֱ��������2��4��6�����ǽ���Ƭ���泯�ϣ�������ϴ�Ⱥ�ÿ�鿨Ƭ�и�����һ�ţ���Ϊһ����Ϸ�������������ſ�Ƭ����������֮��С��10����С����ʤ�������������ſ�Ƭ����������֮������10����С����ʤ������Ϊ�����Ϸ�����˫����ƽ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ���д�һ¥����¥��һ�Զ����ݣ�ͼ2�Dz���ʾ��ͼ����֪�Զ�����AB���¶�Ϊ1��2.4��AB�ij�����13�ף�MN�Ƕ�¥¥����MN��PQ��C��MN�ϴ����Զ����ݶ���B�����Ϸ���һ�㣬BC��MN�����Զ����ݵ�A�����C�������Ϊ37�������¥�IJ��BCԼΪ����ȷ��0.1�ף�sin37���0.60��cos37���0.80��tan37���0.75����������


ͼ1 ͼ2
A. 4�� B. 3.6�� C. 2.2�� D. 4.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
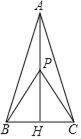
����Ŀ����ͼ����ABC�У���BAC��30����AB��AC��P�ǵױ��ϵĸ�AH��һ�㣮��AP+BP+CP����СֵΪ2![]() ����BC��_____��
����BC��_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com