
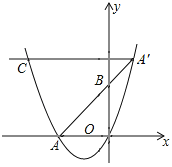
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为_____.
【答案】3
【解析】解方程x2+mx=0得A(﹣m,0),再利用对称的性质得到点A的坐标为(﹣1,0),所以抛物线解析式为y=x2+x,再计算自变量为1的函数值得到A′(1,2),接着利用C点的纵坐标为2求出C点的横坐标,然后计算A′C的长.
当y=0时,x2+mx=0,解得x1=0,x2=﹣m,则A(﹣m,0),
∵点A关于点B的对称点为A′,点A′的横坐标为1,
∴点A的坐标为(﹣1,0),
∴抛物线解析式为y=x2+x,
当x=1时,y=x2+x=2,则A′(1,2),
当y=2时,x2+x=2,解得x1=﹣2,x2=1,则C(﹣2,1),
∴A′C的长为1﹣(﹣2)=3,
故答案为:3.


科目:初中数学 来源: 题型:
【题目】甲、乙两车站相距![]() ,一列慢车从甲站开出,每小时行驶
,一列慢车从甲站开出,每小时行驶![]() ,一列快车从乙站开出,每小时行驶
,一列快车从乙站开出,每小时行驶![]() .(必须用方程解,方程以外的方法不计分)
.(必须用方程解,方程以外的方法不计分)
(1)两车同时开出,相向而行,多少小时相遇?
(2)两车同时开出,同向而行,慢车在前,多少小时快车追上慢车?
查看答案和解析>>
科目:初中数学 来源: 题型:
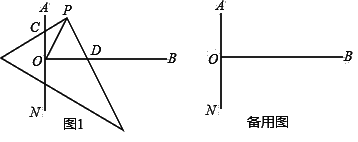
【题目】如图1,射线OB与直线AN垂直于点O,线段OP在∠AOB内,一块三角板的直角顶点与点P重合,两条直角边分别与AN、OB的交于点C、D.
(1)当∠POB=60°,∠OPC=30°,PC=2时,则PD= .
(2)若∠POB=45°,
①当PC与PO重合时,PC和PD之间的数量关系是 ;
②当PC与PO不重合时,猜想PC与PD之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坐标平面上,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC=5.若A点的坐标为(-3,1),B、C两点在方程式y=-3的图形上,D、E两点在y轴上,则F点到y轴的距离为何?( )
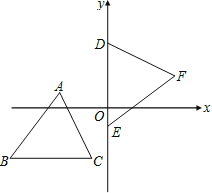
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
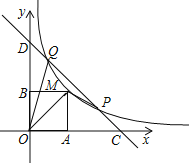
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知有理数![]() 在数轴上所对应的点分别是
在数轴上所对应的点分别是![]() 三点,且
三点,且![]() 满足:①多项式
满足:①多项式![]() 是关于
是关于![]() 的二次三项式:②
的二次三项式:②![]()
![]() 请在图1的数轴上描出
请在图1的数轴上描出![]() 三点,并直接写出
三点,并直接写出![]() 三数之间的大小关系(用“<”连接) ;
三数之间的大小关系(用“<”连接) ;
![]() 点
点![]() 为数轴上
为数轴上![]() 点右侧一点,且点
点右侧一点,且点![]() 到
到![]() 点的距离是到
点的距离是到![]() 点距离的
点距离的![]() 倍,求点
倍,求点![]() 在数轴上所对应的有理数;
在数轴上所对应的有理数;
![]() 点
点![]() 在数轴上以每秒
在数轴上以每秒![]() 个单位长度的速度向左运动,同时点
个单位长度的速度向左运动,同时点![]() 和点
和点![]() 在数轴上分别以每秒
在数轴上分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动(其中
个单位长度的速度向右运动(其中![]() ),若在整个运动的过程中,点
),若在整个运动的过程中,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离差始终不变,求
的距离差始终不变,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )
A. 2 B. 2或![]() C.
C. ![]() 或
或![]() D. 2或
D. 2或![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,数轴上
,数轴上![]() 两点所对应的数分别是
两点所对应的数分别是![]() 和
和![]() .
.
(1)填空:![]() ,
,![]() ;
;
(2)数轴上是否存在点![]() ,
,![]() 点在
点在![]() 点的右侧,且点
点的右侧,且点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点的距离的2倍?若存在,请求出点
点的距离的2倍?若存在,请求出点![]() 表示的数;若不存在,请说明理由;
表示的数;若不存在,请说明理由;
(3)点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 点出发向左运动,同时点
点出发向左运动,同时点![]() 以每秒3个单位的速度从
以每秒3个单位的速度从![]() 点出发向右运动,点
点出发向右运动,点![]() 以每秒4个单位的速度从原点
以每秒4个单位的速度从原点![]() 点出发向左运动.若
点出发向左运动.若![]() 为
为![]() 的中点,当
的中点,当![]() 时,求
时,求![]() 两点之间的距离.
两点之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com