
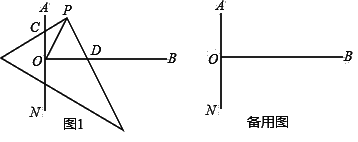
【题目】如图1,射线OB与直线AN垂直于点O,线段OP在∠AOB内,一块三角板的直角顶点与点P重合,两条直角边分别与AN、OB的交于点C、D.
(1)当∠POB=60°,∠OPC=30°,PC=2时,则PD= .
(2)若∠POB=45°,
①当PC与PO重合时,PC和PD之间的数量关系是 ;
②当PC与PO不重合时,猜想PC与PD之间的数量关系,并证明你的结论.
【答案】(1)2![]() (2)①PC=PD;②PC=PD
(2)①PC=PD;②PC=PD
【解析】(1)、作PE⊥AN于E,根据Rt△ECP的性质得出EP的长度,然后根据Rt△OPE的性质求出OP的长度,最后根据等边三角形的性质得出答案;(2)、根据题意得出△PCD为等腰直角三角形,从而得出答案;作PE⊥AN于E,PF⊥OB于F,根据矩形的性质以及角平分线的性质得出△EPC和△FPD全等,从而得出答案.
(1)、作PE⊥AN于E,∵∠POB=60°,OB⊥AN,∴∠AOP=30°,又∠OPC=30°,
∴∠ECP=60°,∴EP=PCsin∠ECP=![]() ,∴OP=2EP=2
,∴OP=2EP=2![]() ,∵∠POB=60°,∠OPD=60°,
,∵∠POB=60°,∠OPD=60°,
∴△POD是等边三角形,∴PD=PO=2![]() ;
;
(2)、①当∠POB=45°时,∵三角板的直角顶点与点P重合,
∴PC与PO重合时,△PCD为等腰直角三角形, ∴PC=PD,
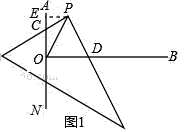
②PC=PD,理由如下:作PE⊥AN于E,PF⊥OB于F,∵AN⊥OB,PE⊥AN,PF⊥OB,
∴四边形EOFP为矩形,∴∠EPF=90°,∴∠EPC=∠FPD,∵∠POB=45°,∴∠POA=45°,
∴OP平分∠EOF,又PE⊥AN,PF⊥OB,∴PE=PF,
在△EPC和△FPD中,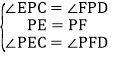 , ∴△EPC≌△FPD, ∴PC=PD.
, ∴△EPC≌△FPD, ∴PC=PD.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
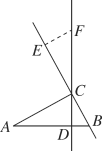
【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)当点E运动多长时间时,CF=AB.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=5,BD=3,则线段CE的长为( )

A. 3 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
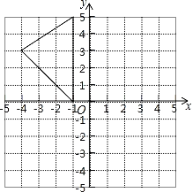
(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC=10cm,BC=12cm,D为BC上一点,连接AD,E为AD上一点,连接BE,若∠ABE=∠BAE═![]() ∠BAC,则DE的长为( )
∠BAC,则DE的长为( )

A.![]() cmB.
cmB.![]() cmC.
cmC.![]() cmD.1cm
cmD.1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
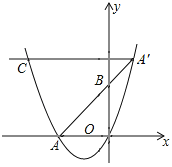
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB∥CD,EG平分∠AEF,EH⊥EG,EH∥GF,则下列结论:①EG⊥GF;②EH平分∠BEF;③FG平分∠EFC;④∠EHF=∠FEH+∠HFD;其中正确的结论个数是( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com