
【题目】学校6名教师和234名学生集体外出活动,准备租用45座大车或30座小车.若租用1辆大车2辆小车共需租车费1000元;若租用2辆大车一辆小车共需租车费1100元.
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名教师,且总租车费用不超过2300元,求最省钱的租车方案.
【答案】
(1)解:设大车每辆的租车费是x元、小车每辆的租车费是y元.
可得方程组 ![]() ,
,
解得 ![]() .
.
答:大车每辆的租车费是400元、小车每辆的租车费是300元
(2)解:由每辆汽车上至少要有1名老师,汽车总数不能大于6辆;
又要保证240名师生有车坐,汽车总数不能小于 ![]() (取整为6)辆,
(取整为6)辆,
综合起来可知汽车总数为6辆.
设租用m辆大型车,则租车费用Q(单位:元)是m的函数,
即Q=400m+300(6﹣m);
化简为:Q=100m+1800,
依题意有:100m+1800≤2300,
∴m≤5,
又要保证240名师生有车坐,45m+30(6﹣m)≥240,解得m≥4,
所以有两种租车方案,
方案一:4辆大车,2辆小车;
方案二:5辆大车,1辆小车.
∵Q随m增加而增加,
∴当m=4时,Q最少为2200元.
故最省钱的租车方案是:4辆大车,2辆小车
【解析】(1)设大车每辆的租车费是x元、小车每辆的租车费是y元.根据题意:“租用1辆大车2辆小车共需租车费1000元”;“租用2辆大车一辆小车共需租车费1100元”;列出方程组,求解即可;(2)根据汽车总数不能小于 ![]() (取整为6)辆,即可求出共需租汽车的辆数;设租用大车m辆,则租车费用Q(单位:元)是m的函数,由题意得出400m+300(6﹣m)≤2300,得出取值范围,分析得出即可.
(取整为6)辆,即可求出共需租汽车的辆数;设租用大车m辆,则租车费用Q(单位:元)是m的函数,由题意得出400m+300(6﹣m)≤2300,得出取值范围,分析得出即可.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】在一张复印出来的纸上,一个三角形的一条边由原图中的2cm变成了6cm,则复印出的三角形的面积是原图中三角形面积的( )
A. 3倍B. 6倍C. 9倍D. 12倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A. 70° B. 70°或86° C. 86° D. 30°或38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE. 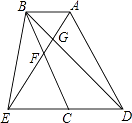
(1)求证:△AFB≌△EFG;
(2)判断CF与AD的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
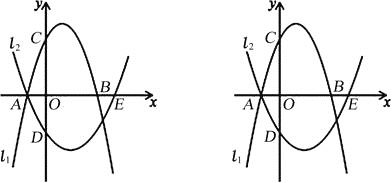
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,F是对角线AC上的一点,点E在BC的延长线上,且BF=EF. 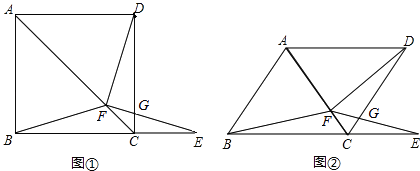
(1)求证:BF=DF;
(2)求证:∠DFE=90°;
(3)如果把正方形ABCD改为菱形,其他条件不变(如图②),当∠ABC=50°时,∠DFE=度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com