Question

【题目】如图①，在正方形ABCD中，F是对角线AC上的一点，点E在BC的延长线上，且BF=EF．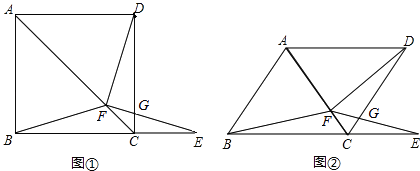
（1）求证：BF=DF；
（2）求证：∠DFE=90°；
（3）如果把正方形ABCD改为菱形，其他条件不变（如图②），当∠ABC=50°时，∠DFE=度．

Answer 1

【答案】
（1）证明：在正方形ABCD中，BC=DC，∠BCF=∠DCF=45°，

∵在△BCF和△DCF中，

，

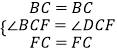∴△BCF≌△DCF（SAS）；

∴BF=DF

（2）证明：∵BF=EF，

∴∠FBE=∠FEB，

又∵∠FBE=∠FDC，

∴∠FEB=∠FDC，

又∵∠DGF=∠EGC，

∴∠DFG=∠ECG=90°，

即∠DFE=90°

（3）50
【解析】（3）证明：由（1）知，△BCF≌△DCF， ∴∠CBF=∠CDF，
∵EE=FB，
∴∠CBF=∠E，
∵∠DGF=∠EGC（对顶角相等），
∴180°﹣∠DGF﹣∠CDF=180°﹣∠EGC﹣∠E，
即∠DFE=∠DCE，
∵AB∥CD，
∴∠DCE=∠ABC，
∴∠DFE=∠ABC=50°，
所以答案是：50．
【考点精析】利用菱形的性质和正方形的性质对题目进行判断即可得到答案，需要熟知菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．