
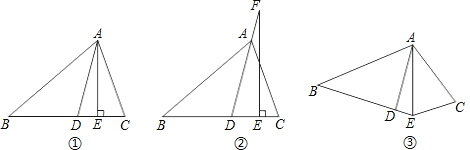
【题目】如图①,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)如图③,若把“AE⊥BC”变成“AE平分∠BEC”,其它条件不变,∠DAE的大小是否变化,并请说明理由.
【答案】(1)∠DAE =15°;(2)∠DFE=15°;(3)∠DAE的度数大小不变.
【解析】
(1)求出∠ADE的度数,利用∠DAE=90°∠ADE即可求出∠DAE的度数;
(2)求出∠ADE的度数,利用∠DFE=90°∠ADE即可求出∠DFE的度数;
(3)利用AE平分∠BEC,AD平分∠BAC,求出∠DFE=15°即是最好的证明.
(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°-∠ADE=15°.
(2)同(1),可得,∠ADE=75°,
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°-∠ADE=15°.
(3)结论:∠DAE的度数大小不变.
证明:∵AE平分∠BEC,
∴∠AEB=∠AEC,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD-∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD-∠DAE=∠B+∠BAD+∠DAE,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴2∠DAE=∠C-∠B=30°,
∴∠DAE=15°.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.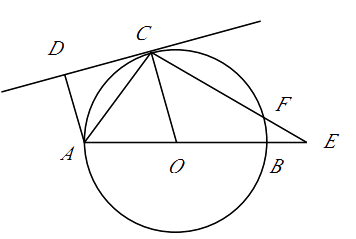
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第块. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某型号跑步机的实物图和示意图,已知踏板CD长为2米,支架AC长为0.8米,CD与地面的夹角为12°,∠ACD=80°,(AB‖ED),求手柄的一端A离地的高度h.(精确到0.1米,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48) 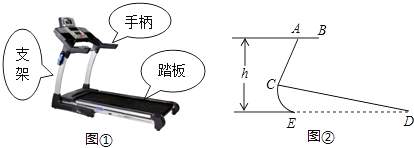
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( ) 
A.50°
B.51°
C.51.5°
D.52.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连结AE、EF、AF,则△AEF的周长为( )

A. 2![]() cm B. 4
cm B. 4![]() cm C. 3
cm C. 3![]() cm D. 3cm
cm D. 3cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com