
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.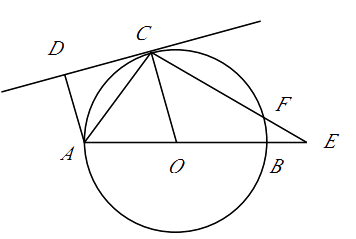
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
【答案】
(1)
解:∵直线与⊙O相切,
∴OC⊥CD;
又∵AD⊥CD,
∴AD//OC,
∴∠DAC=∠OCA;
又∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC;
∴AC平分∠DAO.
(2)
解:①∵AD//OC,∠DAO=105°,
∴∠EOC=∠DAO=105°;
∵∠E=30°,
∴∠OCE=45°.
②作OG⊥CE于点G,可得FG=CG,
∵OC=2![]() ,∠OCE=45°.
,∠OCE=45°.
∴CG=OG=2,
∴FG=2;
∵在RT△OGE中,∠E=30°,
∴GE=2![]() ,
,
∴EF=GE-FG=2![]() -2.
-2.
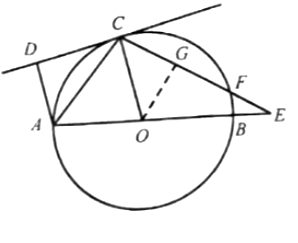
【解析】(1)利用了切线的性质,平行线的判定和性质,等边对等角,角平分线的判定即可得证。
(2)①根据(1)得出的AD//OC,从而得出同位角相等,再利用三角形的内角和定理即可求出答案;②作OG⊥CE于点G,可得FG=CG,根据等边对等角得出CG=OG=FG=2,在根据勾股定理得出GE,从而求出EF=GE-FG.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质),还要掌握三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】学校标准化建设需购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑和每台电子白板各多少万元;
(2)根据学校需要,实际购进电脑和电子白板共30台,总费用30万元,请你通过计算求学校购买了电脑和电子白板各多少台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=﹣ ![]() x﹣1与反比例函数y2=
x﹣1与反比例函数y2= ![]() 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m). 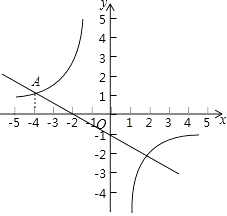
(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .点
.点![]() 的坐标为(
的坐标为(![]() ,0),点
,0),点![]() 的坐标为(
的坐标为(![]() ,0).
,0).
(1)求![]() 的值;
的值;
(2)若点![]() (
(![]() ,
,![]() )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点![]() 运动过程中,试写出
运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究:当![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积为
的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).
(1)作出 ![]() ABC关于原点O成中心对称的
ABC关于原点O成中心对称的 ![]() A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 ![]() A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
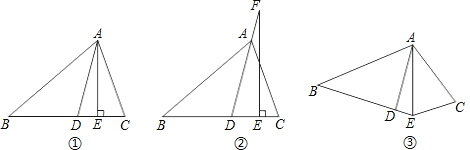
【题目】如图①,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)如图③,若把“AE⊥BC”变成“AE平分∠BEC”,其它条件不变,∠DAE的大小是否变化,并请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com