
【题目】下列方程中,没有实数根的是( )
A.2x+3=0
B.![]() ﹣1=0
﹣1=0
C.![]()
D.![]() +x+1=0
+x+1=0
【答案】D
【解析】解:A、2x+3=0,解得:x=﹣ ![]() ,
,
∴A中方程有一个实数根;
B、在x2﹣1=0中,
△=02﹣4×1×(﹣1)=4>0,
∴B中方程有两个不相等的实数根;
C、 ![]() =1,即x+1=2,
=1,即x+1=2,
解得:x=1,
经检验x=1是分式方程 ![]() =1的解,
=1的解,
∴C中方程有一个实数根;
D、在x2+x+1=0中,
△=12﹣4×1×1=﹣3<0,
∴D中方程没有实数根.
故选D.
【考点精析】关于本题考查的解一元一次方程的步骤和求根公式,需要了解先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC. 
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是形时,四边形OBEC是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.
(1)分别求直线l1与x轴,直线l2与AB的交点坐标;
(2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;
(3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、并三位同学参加数学综合素质测试![]() 各项成绩如下
各项成绩如下![]() 单位:分
单位:分![]()
同学 成绩 | 数与代数 | 图形与几何 | 统计与概率 | 综合与实践 |
甲 | 90 | 93 | 89 | 90 |
乙 | 94 | 92 | 94 | 86 |
丙 | 92 | 91 | 90 | 88 |
![]() 甲、乙、丙三位同学成绩的中位数分别为______;
甲、乙、丙三位同学成绩的中位数分别为______;
![]() 如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师在课堂上提出一个问题:“通过探究知道: ![]() ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用![]() ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
(1)![]() 的小数部分是a,
的小数部分是a, ![]() 的整数部分是b,求a+b﹣
的整数部分是b,求a+b﹣![]() 的值.
的值.
(2)已知8+![]() =x+y,其中x是一个整数,0<y<1,求3x+(y﹣
=x+y,其中x是一个整数,0<y<1,求3x+(y﹣![]() )2018的值.
)2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.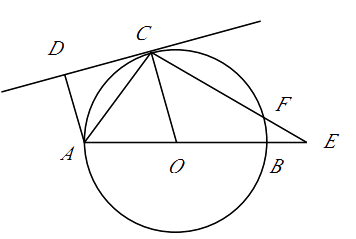
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com