
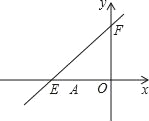
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .点
.点![]() 的坐标为(
的坐标为(![]() ,0),点
,0),点![]() 的坐标为(
的坐标为(![]() ,0).
,0).
(1)求![]() 的值;
的值;
(2)若点![]() (
(![]() ,
,![]() )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点![]() 运动过程中,试写出
运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究:当![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积为
的面积为![]() ,并说明理由.
,并说明理由.

【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
试题(1)将点E坐标(-8,0)代入直线y=kx+6就可以求出k值,从而求出直线的解析式;
(2)由点A的坐标为(-6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)根据△OPA的面积为![]() 代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
(1)∵点E(﹣8,0)在直线y=kx+6上,
∴0=﹣8k+6,
∴k=![]() ;
;
(2)∵k=![]() ,
,
∴直线的解析式为:y=![]() x+6,
x+6,
∵P点在y=![]() x+6上,设P(x,
x+6上,设P(x,![]() x+6),
x+6),
∴△OPA以OA为底的边上的高是|![]() x+6|,
x+6|,
当点P在第二象限时,|![]() x+6|=
x+6|=![]() x+6,
x+6,
∵点A的坐标为(﹣6,0),
∴OA=6.
∴S=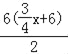 =
=![]() x+18.
x+18.
∵P点在第二象限,
∴﹣8<x<0;
(3)设点P(m,n)时,其面积S=![]() ,
,
则![]() ,
,
解得|n|=![]() ,
,
则n1=![]() 或者n2=﹣
或者n2=﹣![]() (舍去),
(舍去),
当n=![]() 时,
时,![]() =
=![]() m+6,
m+6,
则m=﹣![]() ,
,
故P(﹣![]() ,
,![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙、并三位同学参加数学综合素质测试![]() 各项成绩如下
各项成绩如下![]() 单位:分
单位:分![]()
同学 成绩 | 数与代数 | 图形与几何 | 统计与概率 | 综合与实践 |
甲 | 90 | 93 | 89 | 90 |
乙 | 94 | 92 | 94 | 86 |
丙 | 92 | 91 | 90 | 88 |
![]() 甲、乙、丙三位同学成绩的中位数分别为______;
甲、乙、丙三位同学成绩的中位数分别为______;
![]() 如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:

(1)设装运A种脐橙的车辆数为![]() ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.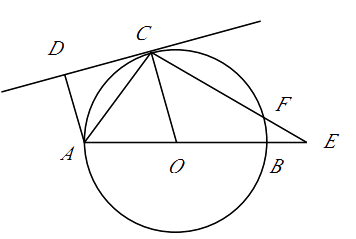
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.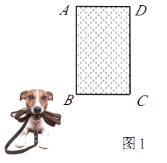
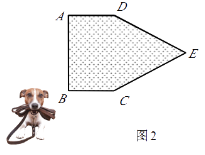
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某型号跑步机的实物图和示意图,已知踏板CD长为2米,支架AC长为0.8米,CD与地面的夹角为12°,∠ACD=80°,(AB‖ED),求手柄的一端A离地的高度h.(精确到0.1米,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48) 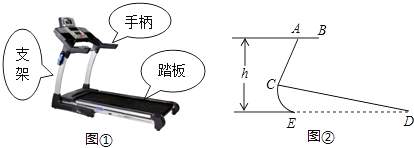
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班同学上数学活动课,利用角尺平分一个角(如图).设计了如下方案:
(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(Ⅱ)∠AOB是一个任意角,在边OA,OB上分别取OM=ON,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com