
【题目】计算下列各题
(1)计算:(﹣1)2014﹣|﹣ ![]() |+
|+ ![]() ﹣(
﹣( ![]() ﹣π)0;
﹣π)0;
(2)先化简,再求值:(2x﹣1)2﹣2(3﹣2x),其中x=﹣2.
【答案】
(1)解:原式=1﹣ ![]() +2
+2 ![]() ﹣1=
﹣1= ![]()
(2)解:原式=4x2﹣4x+1﹣6+4x=4x2﹣5,
把x=﹣2代入原式,得
=4×(﹣2)2﹣5
=11.
【解析】(1)本题涉及零指数幂、乘方、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;(2)根据整式的乘法,可化简代数式,根据代数式求值的方法,可得答案.
【考点精析】利用零指数幂法则和实数的运算对题目进行判断即可得到答案,需要熟知零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);先算乘方、开方,再算乘除,最后算加减,如果有括号,先算括号里面的,若没有括号,在同一级运算中,要从左到右进行运算.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别相交是AB、CD的中点,EF分别交BD、AC于点G、H。求证:OG=OH。
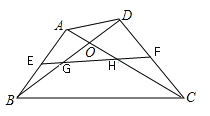
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数![]() 与
与![]() 图象的交于点A,
图象的交于点A,![]() 若点A的坐标为
若点A的坐标为![]() .
.
![]() 点B的坐标为______;
点B的坐标为______;
![]() 若点P为第一象限内双曲线上不同于点B的任意一点.
若点P为第一象限内双曲线上不同于点B的任意一点.
![]() 设直线PA交x轴于点M,直线PB交x轴于点N,求证
设直线PA交x轴于点M,直线PB交x轴于点N,求证![]() ;
;
![]() 当P的坐标为
当P的坐标为![]() 时,连结PO延长交
时,连结PO延长交![]() 于C,求证四边形PACB为矩形.
于C,求证四边形PACB为矩形.
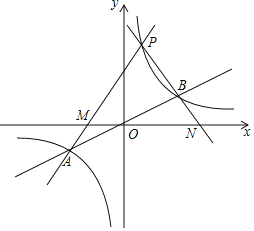
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校标准化建设需购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑和每台电子白板各多少万元;
(2)根据学校需要,实际购进电脑和电子白板共30台,总费用30万元,请你通过计算求学校购买了电脑和电子白板各多少台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() 、
、![]() ,与x轴相交于C点.
,与x轴相交于C点.
![]() 求点A、B的坐标及直线
求点A、B的坐标及直线![]() 的解析式;
的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 观察第一象限的图象,直接写出不等式
观察第一象限的图象,直接写出不等式![]() 的解集;
的解集;
![]() 如图
如图![]() ,在x轴上是否存在点P,使得
,在x轴上是否存在点P,使得![]() 的和最小?若存在,请说明理由并求出P点坐标.
的和最小?若存在,请说明理由并求出P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .点
.点![]() 的坐标为(
的坐标为(![]() ,0),点
,0),点![]() 的坐标为(
的坐标为(![]() ,0).
,0).
(1)求![]() 的值;
的值;
(2)若点![]() (
(![]() ,
,![]() )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点![]() 运动过程中,试写出
运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究:当![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积为
的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要利用28米长的篱笆和一堵最大可利用长为12米的墙围成一个如图1的一边靠墙的矩形养鸡场,在围建的过程中遇到了以下问题,请你帮忙来解决.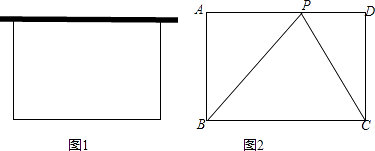
(1)这个矩形养鸡场要怎样建面积能最大?求出这个矩形的长与宽;
(2)在(1)的前提条件下,要在墙上选一个点P,用不可伸缩的绳子分别连接BP,CP,点P取在何处所用绳子长最短?
(3)仍然是矩形养鸡场面积最大的情况下,若把(2)中的不可伸缩的绳子改为可以伸缩且有弹性的绳子,点P可以在墙上自由滑动,求sin∠BPC的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com