
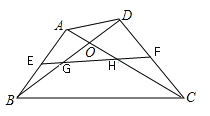
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别相交是AB、CD的中点,EF分别交BD、AC于点G、H。求证:OG=OH。
 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】如图所示,底边BC为2 ![]() ,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )
,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( ) 
A.2+2 ![]()
B.2+ ![]()
C.4
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、并三位同学参加数学综合素质测试![]() 各项成绩如下
各项成绩如下![]() 单位:分
单位:分![]()
同学 成绩 | 数与代数 | 图形与几何 | 统计与概率 | 综合与实践 |
甲 | 90 | 93 | 89 | 90 |
乙 | 94 | 92 | 94 | 86 |
丙 | 92 | 91 | 90 | 88 |
![]() 甲、乙、丙三位同学成绩的中位数分别为______;
甲、乙、丙三位同学成绩的中位数分别为______;
![]() 如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
如果数与代数、图形与几何、统计与概率、综合与实践的成绩按3:3:2:2计算,分别计算甲、乙、丙三位同学的数学综合素质测试成绩,从成绩看,应推荐谁参加更高级别的比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )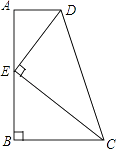
A.CE= ![]() DE
DE
B.CE= ![]() DE
DE
C.CE=3DE
D.CE=2DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某型号跑步机的实物图和示意图,已知踏板CD长为2米,支架AC长为0.8米,CD与地面的夹角为12°,∠ACD=80°,(AB‖ED),求手柄的一端A离地的高度h.(精确到0.1米,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48) 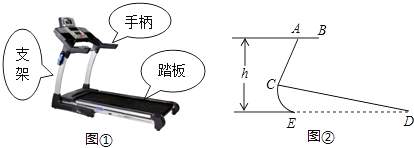
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com