
【题目】如图所示,底边BC为2 ![]() ,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )
,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( ) 
A.2+2 ![]()
B.2+ ![]()
C.4
D.3 ![]()
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ∶∠BOC=( )

A. 1∶2 B. 1∶3 C. 2∶5 D. 1∶4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上和有理数 a、b、c 对应的点的位置如图所示,有下面四个结论:①abc<0;②|a﹣b|+|b﹣c|=|a﹣c|③(a﹣b)(b﹣c)(c﹣a)>0;④|a|<1﹣bc,其中正确的结论有______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,
, ![]() ,结果保留整数.)
,结果保留整数.) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】历史上的数学巨人欧拉最先把关于![]() 的多项式用记号
的多项式用记号![]() 的形式来表示(
的形式来表示(![]() 可用其它字母,但不同的字母表示不同的多项式),例如
可用其它字母,但不同的字母表示不同的多项式),例如![]() ,把
,把![]() =某数时的多项式的值用
=某数时的多项式的值用![]() 来表示.
来表示.
例如![]() 时多项式
时多项式![]() 的值记为
的值记为![]() ,
,
已知![]() ,
,![]()
(1)求![]() 的值
的值
(2)若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC=2 ![]() ,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB= .
,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB= .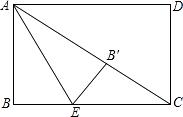
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别相交是AB、CD的中点,EF分别交BD、AC于点G、H。求证:OG=OH。
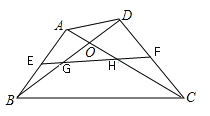
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com